Homework Set 2: Difference between revisions
| (17 intermediate revisions by the same user not shown) | |||
| Line 28: | Line 28: | ||
</math> | </math> | ||
'''(a)''' In the canonical ensemble, | '''(a)''' In the canonical ensemble, find matrix representation of the density operator <math>\hat{\rho}_\mathrm{eq} = e^{-\beta \hat{H}}/Z</math> for <math> \mathbf{B} </math> along the ''z'' axis. | ||
'''(b)''' Repeat the calculation from '''(a)''' assuming that <math> \mathbf{B} </math> points along the ''x'' axis. | '''(b)''' Repeat the calculation from '''(a)''' assuming that <math> \mathbf{B} </math> points along the ''x'' axis. | ||
| Line 36: | Line 36: | ||
== Problem 2: Bloch equation for thermal relaxation and decoherence of a two-level system == | == Problem 2: Bloch equation for thermal relaxation and decoherence of a two-level system == | ||
The [https://journals.aps.org/pr/abstract/10.1103/PhysRev.70.460 Bloch equation] is widely used phenomenological tool to understand relaxation toward thermal equilibrium and decoherence of two-level systems like qubits in quantum computing, spin-1/2 of electrons in spintronics and nuclear spins in medical physics. | The [https://journals.aps.org/pr/abstract/10.1103/PhysRev.70.460 Bloch equation] is widely used phenomenological tool to understand relaxation toward thermal equilibrium and decoherence of two-level systems like qubits in quantum computing, spin-1/2 of electrons in spintronics and nuclear spins in medical physics. | ||
For example, in [https:// | For example, in [https://case.edu/med/neurology/NR/MRI%20Basics.htm MRI imaging of brain and spine] tissue is characterized by two different relaxation times, T<sub>1</sub> and T<sub>2</sub>. T<sub>1</sub> is the so-called longitudinal relaxation time which determines the rate at which excited proton spins return to equilibrium orientation. It is a measure of the time taken for spinning protons to realign with the external magnetic field. T<sub>2</sub> is the so-called transverse relaxation time (or ''decoherence time'' in modern terminology) which determines the rate at which excited protons spins go out of phase with each other. It is a measure of the time taken for spinning protons to lose phase coherence among the nuclei spinning perpendicular to the main field. | ||
Using the language of spin-1/2, the Bloch equation can be written as | Using the language of spin-1/2 in an external magnetic field, the Bloch equation can be written as: | ||
<math> \frac{\partial \hat{\rho}}{\partial t} = -\frac{i}{\hbar} [\hat{H},\hat{\rho}] - \frac{1}{T_1}(\hat{\rho} - \hat{\rho}_\mathrm{eq}) - \frac{1}{ | <math> \frac{\partial \hat{\rho}}{\partial t} = -\frac{i}{\hbar} [\hat{H},\hat{\rho}] - \frac{1}{T_1}(\hat{\rho} - \hat{\rho}_\mathrm{eq}) - \frac{1}{T_2} \begin{pmatrix} | ||
0 & \rho_{\uparrow\downarrow} \\ | 0 & \rho_{\uparrow\downarrow} \\ | ||
\rho_{\downarrow\uparrow} & 0 | \rho_{\downarrow\uparrow} & 0 | ||
\end{pmatrix}, </math> | \end{pmatrix}, </math> | ||
where <math>\hat{\rho}_\mathrm{eq}</math> is the same density matrix in canonical ensemble studied in Problem 1. | where <math>\hat{\rho}_\mathrm{eq}</math> is the same density matrix in canonical ensemble studied in Problem 1 and <math> \hat{H} = -g \mu_B \hat{\sigma}_z B </math> is the Hamiltonian for the z-axis chosen along the magnetic field. Note that although [https://journals.aps.org/pr/abstract/10.1103/PhysRev.70.460 Bloch] did not specify the physical mechanisms giving rise to T<sub>1</sub> and T<sub>2</sub>, he did correctly conclude that T<sub>1</sub> must result from thermal agitation and T<sub>2</sub> from interaction of single spin with neighboring spins. | ||
'''(a)''' Using the fact that arbitrary (pure or mixed) quantum state of spin-1/2 can always be written as: | '''(a)''' Using the fact that arbitrary (pure or mixed) quantum state of spin-1/2 can always be written as: | ||
<math> \hat{\rho} = \frac{1}{2} \left( \hat{I} + \mathbf{P} \cdot \boldsymbol{\sigma | <math> \hat{\rho} = \frac{1}{2} \left( \hat{I} + \mathbf{P} \cdot \boldsymbol{\sigma} \right) </math>, | ||
show that the Bloch equation can be re-written as differential equation for the Bloch vector <math> \mathbf{P} </math>: | show that the Bloch equation can be re-written as differential equation for the Bloch vector <math> \mathbf{P} </math>: | ||
<math> \frac{\partial \mathbf{P}}{\partial t} = \hat{A} \mathbf{P} + \mathbf{C} </math>, | |||
where you should find explicit form of <math> \hat{A} </math> as a 3 x 3 matrix and <math> \mathbf{C} \in {\rm I\!R}^3 </math> as a vector. | |||
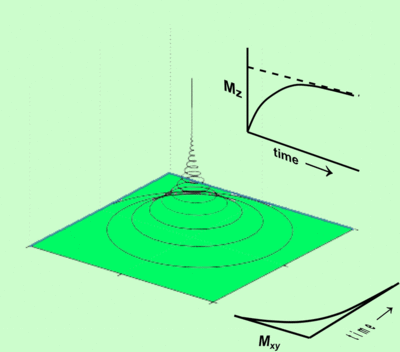
'''(b)''' Solve differential equation for <math> \mathbf{P} </math> assuming the initial condition <math> \mathbf{P}(t=0) \equiv (0,1,0) </math>. For typical situation <math> T_1 \gg T_2 \gg \hbar/(g \mu_B B) </math>, plot your solution using Mathematica and comment on its physical meaning. You should obtain a spiral curve resembling a "tent" show below: | |||
[[Image:bloch_solution.gif|center|400px]] | |||
== Problem 3: Canonical partition function for two-interacting spins== | == Problem 3: Canonical partition function for two-interacting spins== | ||
Latest revision as of 17:37, 8 March 2021
Problem 1: Canonical partition function for a single spin-1/2
The Hamiltonian for an electron spin degree of freedom in the external magnetic field is given by:
where is the Bohr magneton, is the gyromagnetic ratio, and is the vector of the Pauli matrices:
(a) In the canonical ensemble, find matrix representation of the density operator for along the z axis.
(b) Repeat the calculation from (a) assuming that points along the x axis.
(c) Calculate the average energy in each of the above cases.
Problem 2: Bloch equation for thermal relaxation and decoherence of a two-level system
The Bloch equation is widely used phenomenological tool to understand relaxation toward thermal equilibrium and decoherence of two-level systems like qubits in quantum computing, spin-1/2 of electrons in spintronics and nuclear spins in medical physics. For example, in MRI imaging of brain and spine tissue is characterized by two different relaxation times, T1 and T2. T1 is the so-called longitudinal relaxation time which determines the rate at which excited proton spins return to equilibrium orientation. It is a measure of the time taken for spinning protons to realign with the external magnetic field. T2 is the so-called transverse relaxation time (or decoherence time in modern terminology) which determines the rate at which excited protons spins go out of phase with each other. It is a measure of the time taken for spinning protons to lose phase coherence among the nuclei spinning perpendicular to the main field.
Using the language of spin-1/2 in an external magnetic field, the Bloch equation can be written as:
where is the same density matrix in canonical ensemble studied in Problem 1 and is the Hamiltonian for the z-axis chosen along the magnetic field. Note that although Bloch did not specify the physical mechanisms giving rise to T1 and T2, he did correctly conclude that T1 must result from thermal agitation and T2 from interaction of single spin with neighboring spins.
(a) Using the fact that arbitrary (pure or mixed) quantum state of spin-1/2 can always be written as:
,
show that the Bloch equation can be re-written as differential equation for the Bloch vector :
,
where you should find explicit form of as a 3 x 3 matrix and as a vector.
(b) Solve differential equation for assuming the initial condition . For typical situation , plot your solution using Mathematica and comment on its physical meaning. You should obtain a spiral curve resembling a "tent" show below:
Problem 3: Canonical partition function for two-interacting spins
In some antiferromagnetic materials, such as , spins are arranged in pairs. To first approximation, such dimers can be considered independently of each other. The Hamiltonian of a single dimer in the external magnetic field is given by:
where is the exchange coupling constant and is the Bohr magneton.
(a) How many energy eigenlevels does this Hamiltonian have? List all eigenergies explicitly.
(b) Using your result in (a), compute the canonical partition function and free energy of dimers, as well as find their entropy.
HINT: An equivalent pedagogical expression for the Hamiltonian above is given by:
.
Problem 4: Density matrix and canonical partition function for one-dimensional harmonic oscillator
Consider a single one-dimensional quantum harmonic oscillator described by the Hamiltonian:
,
where .
(a) Find the partition function in the quantum canonical ensemble at temperature .
(b) Using the result from (a), calculate the averge energy .
(c) Write down the formal expression for the canonical density operator in terms of the eigenstates of the Hamiltonian and the corresponding energy levels .
(d) Using the result in (c), write down the density matrix in the coordinate representation .
(e) In the coordinate representation, calculate explicitly in the high temperature limit .
HINT: One approach is to utilize the following result
which you can apply to the Boltzmann operator:
while neglecting terms of order and higher since is very small in the high temperature limit.
(f) At low temperatures, is dominated by low-energy states. Use the ground state wave function only, evaluate the limiting behavior of as .