Homework Set 2
Problem 1: Tight-binding Hamiltonian of triatomic molecule

Consider a molecule made out of three atoms with a single valence orbital per atom, for , as shown in the Figure. These atoms share one delocalized electron when chemically bonded.
- (a) When three atoms are far away from each other and, therefore, not bonded, electron resides on one of them in lowest energy state . Write Hamiltonian matrix for this situation. What is the degeneracy of the ground state energy of this Hamiltonian?
- (b) When three atoms are sufficiently close, electron can tunnel through Coulomb potential barriers generated by atoms with a hopping parameter denoted in the Figure. Write Hamiltonian matrix for such covalently bonded molecule and diagonalize it to find its eigeneneries and eignestates.
- (c) What is the degeneracy of eigenvalues found in (b)? Specify which geometrical symmetry of the molecule is responsible for degeneracy.
Problem 2: Tight-binding Hamiltonian of one-dimensional nanowire on the lattice with a basis
Consider a tight-binding model of a 1D nanowire:
,
The integer is indexing sites at which the atoms are located. The distance between two sites defines the lattice spacing , while the nearest neighbor hopping sets the unit of energy. The ket is quantum state of an electron on atom , so that is the corresponding wave function in coordinate representation (or single "orbital" per site) which decays fast away from the position of an atom .
- (a) What is the periodicity of the Hamiltonian? (That is, after how many sites the chain starts to repeat itself? The atoms on those sites define the unit cell of the wire whose periodic repetition in both direction generates the whole wire.)
- (b) Use the Bloch theorem to reduce the eigenvalue problem of an infinite matrix , obtained by representing the Hamiltonian in the basis of orbitals , to diagonalization of a small matrix [whose size is equal to the periodicity of the Hamiltonian found in (a)].
- (c) The matrix in (b) will depended on the Bloch wave vector . For each value of , diagonalize this matrix and plot bands where vector belongs to the first Brillouin zone (this task will have to be carried our numerically).
Problem 3: Density of states of tight-binding Hamiltonian of one-dimensional nanowire with a single impurity
A nanowire consists of 500 atoms described by a 1D tight-binding Hamiltonian:
.
- (a) Compute numerically the density (DOS) of states for this wire assuming periodic boundary conditions and . In numerical calculations use as the unit of energy. How does DOS change if you increase the number of atoms from 500 to 5000?
- (b) Replacement of the original atom in the middle of the chain by an impurity atom can be modeled by using . Compute (DOS) for this case and comment on differences between (a) and (b). What is the highest eigenenergy in (a) vs. (b)? What is the physical meaning of this energy in the case (b)?
- (c) Use the Green function method to compare its result for DOS to (a) and (b) obtained using eigenvalue method for 500 atom wire.
Problem 4: Hofstadter butterfly of electrons on square tight-binding lattice in external magnetic field
The Hofstadter butterfly is the energy spectrum of an infinite square lattice plotted as a function of the magnetic field. In this problem we will examine similar spectra for finite lattices modeling arrays of quantum dots in a magnetic field using methods that consider the appropriate molecular orbitals and compare their spectra to the Hofstadter butterfly.
- (a) Reproduce panels (a)-(f) in Fig. 5 of American Journal of Physics 72, 5 (2004) for small arrays up to .
- (b) If you increase your quantum dot array size to , does your plot resemble Hofstadter butterfly on an infinite lattice plotted in Fig. 6 of the same reference as in (a).
Problem 5: Shubnikov-de Haas oscillations in two-dimensional electron gas
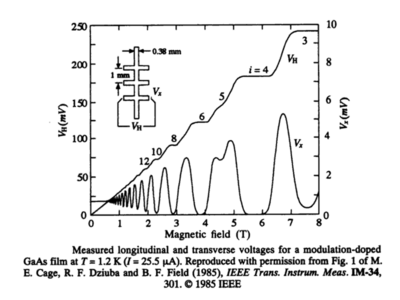
The physical properties of a two-dimensional electron gas (2DEG), in semiconductor heterostructures or within 2D materials, can be measured by embedding it into a multiterminal Hall bridge, as shown in the Figure above. The energy spectrum of 2D electrons in magnetic field orthogonal to such bridge consists of discrete Landau lavels:
,
which are well-separated for large enough B. Thus, the step-like density of states associated with 2DEG ( is the lowest level in the triangular potential that confines 2DEG) is then broken up into a series of peaks spaced by :
. (1)
Although the spikes are ideally delta functions, scattering processes spread them out in energy. As one changes the magnetic field B, longitudinal voltage (from which one computes the longitudinal resisitivity ) in the Figure above goes through one cycle of oscillations as the Fermi energy moves from the center of one Landau level to the center of the next Landau level. These oscillations are refered to as the Shubnikov-de Haas (SdH) oscillations.
- (a) Devise a procedure that will allow you to extract electron density in 2DEG from the values of magnetic field B at which (or the corresponding ) reaches maximum in the course of SdH oscillations.
- (b) What is for the 2DEG in the Figure above?
HINT: From Eq. (1) we see that the number of occupied Landau levels is , if electron density is already known.
Problem 6: Full surface of energy-momentum dispersion in graphene and its Dirac cone approximation at selected points in the Brillouin zone
The energy momentum-dispersion of graphene valence and conduction bands is given by the formula derived in class:
which assumes tight-binding Hamiltonian projected to a basis set of single orbital per carbon atom and hopping allowed only between the nearest neighbor carbon atoms. The honeycomb lattice spacing is .
- (a) Using Python or Mathematica plot this function as a surface in 3D k-space within the range of vector values defined by the first Brillouin zone.
- (b) Near one of the two inequivalent K points [the so-called Dirac points at which ] in the corners of the first Brillouin zone, where the conduction (top surface) and valence (bottom surface) bands touch, the dispersion has a conical shape characteristics of massless relativistic particles, such as photons or neutrinos. Up to what energy away from the Dirac point (which is the Fermi energy of ideal undoped graphene) can the real dispersion shown in your figure be approximated by linear dispersion of the "Dirac cones"? You can subtract surface around one of the K points from the conical surface (corrections are ; here and the Fermi velocity is ) and find at which energy their difference starts to be more than 5%.
Problem 7: Density of state of graphene flake
The honeycomb lattice of graphene is topologically equivalent to a brick lattice shown in the Figure below:

Thus, the matrix representation of the Hamiltonian defined on this lattice can be obtained in the same fashion as for the square lattice (used in Problem 4. of Homework Set 2), i.e., by loading its submatrices describing graphene supercells coupled to adjacent supercells via the hopping submatrices . The carbon atoms within the supercells as well as the structure of these submatrices are shown in the Figure. Here it is assumed that electron can hop between only the nearest neighbor carbon atoms with probability .
- (a) Using the honeycomb (or equivalent brick) lattice of carbon atoms (for example, the honeycomb lattice in the top inset of the Figure above is in this terminology), construct the full Hamiltonian matrix of finite size graphene sheet and compute its density of states (DOS) via the Green function method used in Homework Set 2 in the energy range .
- (b) Introduce periodic boundary into (this requires to input two additional submatrices into , as well as to introduce extra hoppings into ) and compute its DOS via the same method as in (a).
- (c) Does any of your numerically obtained DOS for finite-size graphene sheet resembles analytical DOS shown in Fig. 5 (page 114) of Rev. Mod. Phys. 81, 109 (2009). [PDF]?