Project 3: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
A linear chain of point masses coupled by harmonic springs is a standard model used to introduce various concepts of solid state physics. | A linear chain of point masses coupled by harmonic springs is a standard model used to introduce various concepts of solid state physics. | ||
[[Image:chain.gif|thumb|center|400px| | [[Image:chain.gif|thumb|center|400px|An illustration of a linear chain of masses with periodic boundary conditions which effectively connect first and last mass by a spring.]] | ||
The ordered chain has sinusoidal standing wave normal modes (if the ends are fixed) or traveling wave normal modes (if the ends are connected in a ring via periodic or, the so-called, Born-Von Karman boundary conditions). Ballistically (i.e., without any scattering) propagating wave packets can be built from these normal modes, and illustrate the mechanism of heat propagation in insulating crystals. When disorder is introduced in the chain, as simulated by random spring constants <math> K_n </math> in the Figure above (or random masses), qualitatively new effects arise: on length scales longer than the localization length, energy is trapped in few atoms unless there are nonlinear forces [for more details on localization in disordered chains see References below]. | |||
P | |||
Revision as of 15:46, 12 March 2012
Vibrational modes of glasses: The effects of disorder and nonlinearity
A linear chain of point masses coupled by harmonic springs is a standard model used to introduce various concepts of solid state physics.
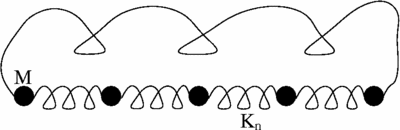
The ordered chain has sinusoidal standing wave normal modes (if the ends are fixed) or traveling wave normal modes (if the ends are connected in a ring via periodic or, the so-called, Born-Von Karman boundary conditions). Ballistically (i.e., without any scattering) propagating wave packets can be built from these normal modes, and illustrate the mechanism of heat propagation in insulating crystals. When disorder is introduced in the chain, as simulated by random spring constants in the Figure above (or random masses), qualitatively new effects arise: on length scales longer than the localization length, energy is trapped in few atoms unless there are nonlinear forces [for more details on localization in disordered chains see References below].
P