Topics

How to select a good topic and style of presentation (for the format and goals of PHYS800):

• Pick a topic that is of relevance to your research or your broader field. It does not have to be too advanced -> it could be something that is missing, or it is improperly covered, in standard textbooks.
• Pick a model on which your topic can be clearly explained, with all details included. Examples from previous presentations include: one or few qubits; one or few spins; one or two atoms, or an infinite tight-binding chain; Hubbard dimer; etc.
• Present using: traditional blackboard; handwritten notes in PDF format which can be annotated as you talk; PPT slides; Jupyter (or Mathematica) notebook in case you are using code snippets to run numerical (or analytical) calculations on simple models.

Quantum Mechanics

Fundamentals

• M. T. Ahari, G. Ortiz, and B. Seradjeha, On the role of self-adjointness in the continuum formulation of topological quantum phases, Am. J. Phys. 84, 858 (2016). [PDF]
• M. M. Nieto, Quantum phase and quantum phase operators: Some physics and some history, Phys. Scr. T48, 5 (1993). [PDF]
• A. C. Hirshfeld and P. Henselder, Deformation quantization in the teaching of quantum mechanics, Am. J. Phys. 70, 537 (2002). [PDF]

Algebraic approach via operators and their functions

• Quantum Mechanics done right graduate course videos by Prof. J. K. Freericks
• E. Munguía-González, S. Rego, and J. K. Freericks, Making squeezed-coherent states concrete by determining their wavefunction, Am. J. Phys. 89, 885 (2021). [PDF]
• A. M. Orjuela and J. K. Freericks, Free expansion of a Gaussian wavepacket using operator manipulations, Am. J. Phys. 91, 463 (2023). [PDF]

Time-evolution

• Decompositions of ordered operator exponentials for time-evolution in computational quantum physics
• L. A. J. Guttieres, M. D. Petrović, J. K. Freericks, Computational projects with the Landau–Zener problem in the quantum mechanics classroom, Am. J. Phys. 91, 885 (2023). [PDF]
• R. Merlin, Rabi oscillations, Floquet states, Fermi's golden rule, and all that: Insights from an exactly solvable two-level model, Am. J. Phys. 89, 26 (2021). [PDF]
• S. Blanes, F. Casas, J. A. Oteo, and J. Ros, A pedagogical approach to the Magnus expansion, Eur. J. Phys. 31, 907 (2010). [PDF]
• C. J. Eckhardt, G. Passetti, M. Othman, C. Karrasch, F. Cavaliere, M. A. Sentef, and D. M. Kennes, Quantum Floquet engineering with an exactly solvable tight-binding chain in a cavity, Commun. Phys. 5, 122 (2022). [PDF]
• M. S. Rudner and N. H. Lindner, The Floquet engineer's handbook, arXiv:2003.08252.

Quantum Optics

• M. Bina, The coherent interaction between matter and radiation: A tutorial on the Jaynes-Cummings model, Eur. Phys. J. Special Topics 203, 163 (2012). [PDF]
• 50 years of Jaynes-Cummings physics
• G. Grynberg, A. Aspect, and Claude Fabre, Introduction to Quantum Optics: From the Semi-classical Approach to Quantized Light (Cambridge University Press, Cambridge, 2010). [PDF]
• Map of Quantum Optics:

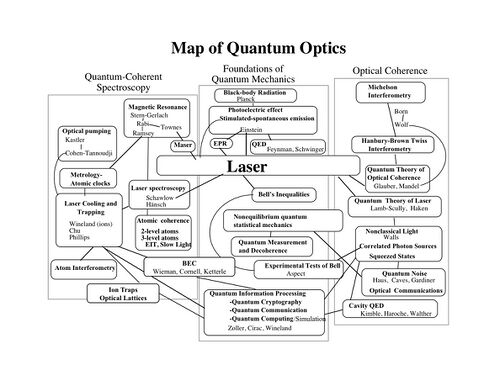
Quantum-Classical Methods

• F. Agostini and B. F. E. Curchod, Different flavors of nonadiabatic molecular dynamics, WIREs Comput. Mol. Sci. 9, e1417 (2019). [PDF]
• F. Agostini, An exact-factorization perspective on quantum-classical approaches to excited-state dynamics, Euro. Phys. J. B 91, 143 (2018). [PDF]

Quantum Information Science

• A. Ekert and P. L. Knight, Entangled quantum systems and the Schmidt decomposition, Am. J. Phys. 63, 415 (1995). [PDF]
• T. Grover, Highly entangled quantum matter [Video]

Open Quantum Systems via Quantum Master Equations

• F. Campaioli, J. H. Cole, and H. Hapuarachchi, Tutorial on quantum master equations: Tips and tricks for quantum optics, quantum computing and beyond, PRX QUANTUM 5, 020202 (2024). [PDF] + Python scripts
• D. Manzano, A short introduction to the Lindblad master equation, AIP Adv. 10, 025106 (2020). [PDF]
• F. Nathan and M. S. Rudner, Universal Lindblad equation for open quantum systems, Phys. Rev. B 102, 115109 (2020). [PDF]
• Y. Tanimura, Numerically “exact” approach to open quantum dynamics: The hierarchical equations of motion (HEOM), J. Chem. Phys. 153, 020901 (2020). [PDF]

Decoherence

• B. Gu and I. Franco, When can quantum decoherence be mimicked by classical noise?, J. Chem. Phys. 151, 014109 (2019). [PDF]
• J. Kincaida, K. McLelland, and M. Zwolak, Measurement-induced decoherence and information in double-slit interference, Am. J. Phys. 84, 522 (2016). [PDF]

Quantum Many-Body Systems

Many-body quantum spin systems

• B. K. Nikolić, From Hubbard dimer to effective antiferromagnetic Hubbard model for two spins
• B. K. Nikolić, Ground state and low-energy magnon excitations of ferro- and antiferromagnets
• K. Joel, D. Kollmar, and L. F. Santos, An introduction to the spectrum, symmetries, and dynamics of spin-1/2 Heisenberg chains, Am. J. Phys. 81, 450 (2013). [PDF]
• F. Mila, Quantum spin liquids, Eur. J. Phys. 21, 499 (2000). [PDF]
• P. Wrzosek, K. Wohlfeld, D. Hofmann, T. Sowiński, and M. A. Sentef, Quantum walk versus classical wave: Distinguishing ground states of quantum magnets by spacetime dynamics, Phys. Rev. B 102, 024440 (2020). [PDF]
• M. Hoffmann and S. Blügel, Systematic derivation of realistic spin models for beyond-Heisenberg solids, Phys. Rev. B 101, 024418 (2020). [PDF]
• S. Kitamura, T. Oka, and H. Aoki, Probing and controlling spin chirality in Mott insulators by circularly polarized laser, Phys. Rev. B 96, 014406 (2017). [PDF]
• A. Szilva, Y. Kvashnin, E. A. Stepanov, O. Eriksson, A. I. Lichtenstein, and M. I. Katsnelson, Quantitative theory of magnetic interactions in solids, Rev. Mod. Phys. 95, 035004 (2023). [PDF]

Computational algorithms

• G. Catarina and B. Murta, Density-matrix renormalization group: a pedagogical introduction, Eur. Phys. J. B 96, 111 (2023). [PDF]
• J. Hauschild and F. Pollmann, Efficient numerical simulations with Tensor Networks: Tensor Network Python (TeNPy), SciPost Phys. Lect. Notes 5 (2018). [PDF]

Path Integrals

• D. H. Rischke, "In-out" (or Feynman) path integrals in quantum mechanics [PDF]
• Y. BenTov, "In-in" (or Schwinger-Keldysh) path integral for the quantum harmonic oscillator, arXiv:2102.05029

Quantum Field Theory

• A. Wurm and M. Berg, Wick calculus, Am. J. Phys. 76, 65 (2008). [PDF]
• G. Fletcher, Functional integrals and the BCS theory of superconductivity, Am. J. Phys. 58, 50 (1990). [PDF]
• K. Byczuk and P. Jakubczyk, Generalized Gaussian integrals with application to the Hubbard–Stratonovich transformation, Am. J. Phys. 91, 840 (2023). [PDF]
• Y. Tanizaki, Y. Hidaka, and T. Hayata, Lefschetz-thimble analysis of the sign problem in one-site fermion model, New J. Phys. 18, 033002 (2016). [PDF]

Numeric and Symbolic Packages

• SNEG Mathematica package for analytical calculations in second quantization.
• QuSpin Python package for numerical calculations (exact diagonalization and quantum dynamics) of arbitrary boson, fermion and spin many-body systems.
• HOQST Julia package for numerical calculations of time evolution of open quantum systems, such as qubits in dissipative environment.
• QuTiP Python package for numerical calculations of time evolution of open quantum systems, such as qubits in dissipative environment.
  • How to install QuTiP from Anaconda:

conda config --append channels conda-forge
conda install qutip

• TeNPy Python package for strongly correlated quantum systems with tensor networks.