Topics

How to select a good topic and style of presentation (for the format and goals of PHYS800):

-> Pick a topic that is of relevance to your research or your broader field. It does not have to be too advanced, so it could be something that is missing, or it is improperly covered, in standard textbooks. 
-> Pick a model on which your topic can be clearly explained, with all details included. Examples from previous presentations include: one or few qubits; one or few spins; one or two atoms, or an infinite tight-binding chain; Hubbard dimer; etc.  
-> Present using: traditional blackboard; handwritten notes in PDF format which can be annotated as you talk; PPT slides; Jupyter (or Mathematica) notebook in case you are using code snippets to run numerical (or analytical) calculations on simple models. 

Quantum Mechanics

Fundamentals

• B. Blankleider and A. N. Kvinikhidze, Shortest derivation of time-independent perturbation theory, Am. J. Phys. 93, 652 (2025). [PDF]
• M. T. Ahari, G. Ortiz, and B. Seradjeha, On the role of self-adjointness in the continuum formulation of topological quantum phases, Am. J. Phys. 84, 858 (2016). [PDF]
• M. M. Nieto, Quantum phase and quantum phase operators: Some physics and some history, Phys. Scr. T48, 5 (1993). [PDF]
• A. C. Hirshfeld and P. Henselder, Deformation quantization in the teaching of quantum mechanics, Am. J. Phys. 70, 537 (2002). [PDF]

Algebraic approach via operators and their identities

• Quantum Mechanics done right graduate course videos by Prof. J. K. Freericks
• E. Munguía-González, S. Rego, and J. K. Freericks, Making squeezed-coherent states concrete by determining their wavefunction, Am. J. Phys. 89, 885 (2021). [PDF]
• A. M. Orjuela and J. K. Freericks, Free expansion of a Gaussian wavepacket using operator manipulations, Am. J. Phys. 91, 463 (2023). [PDF]

Time-evolution

• Overview of decompositions of ordered operator exponentials for time-evolution of quantum systems
• L. A. J. Guttieres, M. D. Petrović, J. K. Freericks, Computational projects with the Landau–Zener problem in the quantum mechanics classroom, Am. J. Phys. 91, 885 (2023). [PDF]
• R. Merlin, Rabi oscillations, Floquet states, Fermi's golden rule, and all that: Insights from an exactly solvable two-level model, Am. J. Phys. 89, 26 (2021). [PDF]
• S. Blanes, F. Casas, J. A. Oteo, and J. Ros, A pedagogical approach to the Magnus expansion, Eur. J. Phys. 31, 907 (2010). [PDF]
• C. J. Eckhardt, G. Passetti, M. Othman, C. Karrasch, F. Cavaliere, M. A. Sentef, and D. M. Kennes, Quantum Floquet engineering with an exactly solvable tight-binding chain in a cavity, Commun. Phys. 5, 122 (2022). [PDF]
• M. S. Rudner and N. H. Lindner, The Floquet engineer's handbook, arXiv:2003.08252.

Open Quantum Systems

• F. Campaioli, J. H. Cole, and H. Hapuarachchi, Tutorial on quantum master equations: Tips and tricks for quantum optics, quantum computing and beyond, PRX QUANTUM 5, 020202 (2024). [PDF] + Python scripts
• D. Manzano, A short introduction to the Lindblad master equation, AIP Adv. 10, 025106 (2020). [PDF]
• F. Nathan and M. S. Rudner, Universal Lindblad equation for open quantum systems, Phys. Rev. B 102, 115109 (2020). [PDF]
• Y. Tanimura, Numerically “exact” approach to open quantum dynamics: The hierarchical equations of motion (HEOM), J. Chem. Phys. 153, 020901 (2020). [PDF]

Decoherence

• B. Gu and I. Franco, When can quantum decoherence be mimicked by classical noise?, J. Chem. Phys. 151, 014109 (2019). [PDF]
• J. Kincaida, K. McLelland, and M. Zwolak, Measurement-induced decoherence and information in double-slit interference, Am. J. Phys. 84, 522 (2016). [PDF]

Quantum Information Science

• A. Ekert and P. L. Knight, Entangled quantum systems and the Schmidt decomposition, Am. J. Phys. 63, 415 (1995). [PDF]
• T. Grover, Highly entangled quantum matter [Video]

Quantum Optics

• M. Bina, The coherent interaction between matter and radiation: A tutorial on the Jaynes-Cummings model, Eur. Phys. J. Special Topics 203, 163 (2012). [PDF]
• 50 years of Jaynes-Cummings physics
• G. Grynberg, A. Aspect, and Claude Fabre, Introduction to Quantum Optics: From the Semi-classical Approach to Quantized Light (Cambridge University Press, Cambridge, 2010). [PDF]
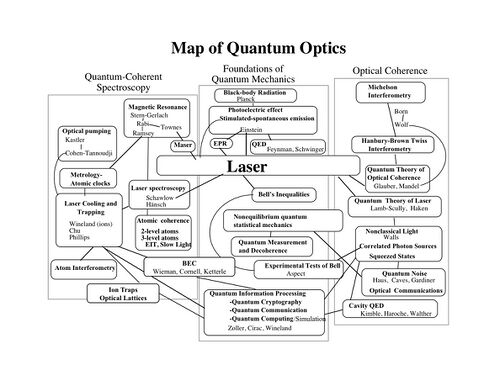
• Map of Quantum Optics:

Quantum-Classical Methods (particularly in Chemical Physics or Physical Chemistry)

• F. Agostini and B. F. E. Curchod, Different flavors of nonadiabatic molecular dynamics, WIREs Comput. Mol. Sci. 9, e1417 (2019). [PDF]
• F. Agostini, An exact-factorization perspective on quantum-classical approaches to excited-state dynamics, Euro. Phys. J. B 91, 143 (2018). [PDF]

Topological concepts in quantum materials

• D. C. Ralph, Berry curvature, semiclassical electron dynamics, and topological materials: Lecture notes for Introduction to Solid State Physics, arXiv:2001.04797 [PDF]

Quantum Many-Body Systems

Quantum spins and magnets

• B. K. Nikolić, From Hubbard dimer to effective antiferromagnetic Hubbard model for two spins
• B. K. Nikolić, Ground state and low-energy magnon excitations of ferro- and antiferromagnets
• K. Joel, D. Kollmar, and L. F. Santos, An introduction to the spectrum, symmetries, and dynamics of spin-1/2 Heisenberg chains, Am. J. Phys. 81, 450 (2013). [PDF]
• F. Mila, Quantum spin liquids, Eur. J. Phys. 21, 499 (2000). [PDF]
• P. Wrzosek, K. Wohlfeld, D. Hofmann, T. Sowiński, and M. A. Sentef, Quantum walk versus classical wave: Distinguishing ground states of quantum magnets by spacetime dynamics, Phys. Rev. B 102, 024440 (2020). [PDF]
• M. Hoffmann and S. Blügel, Systematic derivation of realistic spin models for beyond-Heisenberg solids, Phys. Rev. B 101, 024418 (2020). [PDF]
• S. Kitamura, T. Oka, and H. Aoki, Probing and controlling spin chirality in Mott insulators by circularly polarized laser, Phys. Rev. B 96, 014406 (2017). [PDF]
• A. Szilva, Y. Kvashnin, E. A. Stepanov, O. Eriksson, A. I. Lichtenstein, and M. I. Katsnelson, Quantitative theory of magnetic interactions in solids, Rev. Mod. Phys. 95, 035004 (2023). [PDF]

Superconductivity

• Bogoliubov-de Gennes equations via KWANT

Computational algorithms

• G. Catarina and B. Murta, Density-matrix renormalization group: a pedagogical introduction, Eur. Phys. J. B 96, 111 (2023). [PDF]
• J. Hauschild and F. Pollmann, Efficient numerical simulations with Tensor Networks: Tensor Network Python (TeNPy), SciPost Phys. Lect. Notes 5 (2018). [PDF]

Path Integrals

• D. H. Rischke, "In-out" (or Feynman) path integrals in quantum mechanics [PDF]
• Y. BenTov, "In-in" (or Schwinger-Keldysh) path integral in quantum mechanics, arXiv:2102.05029 (2021). [PDF]

Quantum Field Theory (for AMO and Condensed Matter Physics)

• G. Fletcher, Functional integrals and the BCS theory of superconductivity, Am. J. Phys. 58, 50 (1990). [PDF]
• K. Byczuk and P. Jakubczyk, Generalized Gaussian integrals with application to the Hubbard–Stratonovich transformation, Am. J. Phys. 91, 840 (2023). [PDF]
• Y. Tanizaki, Y. Hidaka, and T. Hayata, Lefschetz-thimble analysis of the sign problem in one-site fermion model, New J. Phys. 18, 033002 (2016). [PDF]
• P. Millington and P. M Saffin, Visualising quantum effective action calculations in zero dimensions, J. Phys. A: Math. Theor. 52, 405401 (2019). [PDF]

Numeric and Symbolic Packages

• SNEG Mathematica package for analytical calculations in second quantization.
• QuSpin Python package for numerical calculations (exact diagonalization and quantum dynamics) of arbitrary boson, fermion and spin many-body systems.
• HOQST Julia package for numerical calculations of time evolution of open quantum systems, such as qubits in dissipative environment.
• QuTiP Python package for numerical calculations of time evolution of open quantum systems, such as qubits in dissipative environment.
  • How to install QuTiP from Anaconda:

conda config --append channels conda-forge
conda install qutip

• TeNPy Python package for strongly correlated quantum systems with tensor networks.