Topics

From phys800
Jump to navigationJump to search

From The Beautiful Cure: The Revolution in Immunology and What it Means for Your Health by Daniel M. Davis (Professor of Immunology with a Ph.D. in physics): 

 “Science is many things. A method, a journey, a route to power, a body of knowledge, a thing you loved or hated at school, a jigsaw puzzle with an infinite number of pieces, a force for good and bad which has produced both food and bombs. Arguably, its greatest success has been, and will be for some time to come, in curing diseases.”

Frank Wilczek on Einstein's productive years: 

 “The later part of Einstein’s career-more than half, chronologically, covering thirty years—was devoted to (let’s call it) Theory of Everything physics, and it was essentially fruitless. During Einstein’s great creative period he dealt with much more specific, less grandiose problems. His special theory of relativity came out of worrying about technical difficulties in the electrodynamics of moving bodies. His general theory of relativity came out of worrying about how to make a theory of gravity consistent with special relativity. His pioneering work on Brownian motion and Bose-Einstein statistics came out of worrying about the relationship between fundamental physics and thermodynamics; specifically, about fluctuations. His seminal work on photons came out of thinking about specific, puzzling experimental results, notably the observed spectrum of blackbody radiation.”

Frank Wilczek on Einstein's unproductive years: 

 “Why did Einstein loathe the implications of quantum mechanics? This question belongs to psychology more than physics. There was certainly no empirical reason for his distaste-on the contrary, quantum mechanics went from success to brilliant success. Einstein apparently just didn’t like the way probability enters into the laws of quantum theory, and he may have sensed difficulties in reconciling quantum theory with his baby, relativity. A normal scientific reaction would have been to respect the overwhelming success of what people were doing in quantum theory, assimilate that work, and try to tinker with it (maybe hoping to remove the probabilities) or build on it (to include relativity). In fact, we know that great results were there to be had along those directions, such as the Bell inequalities and the Dirac equation. But instead of trying to tinker or build, Einstein went into denial.”

Quantum Mechanics

Fundamentals

  • M. T. Ahari, G. Ortiz, and B. Seradjeha, On the role of self-adjointness in the continuum formulation of topological quantum phases, Am. J. Phys. 84, 858 (2016). [PDF]
  • M. M. Nieto, Quantum Phase and quantum phase operators: Some physics and some history, Phys. Scr. T48, 5 (1993). [PDF]
  • A. C. Hirshfeld and P. Henselder, Deformation quantization in the teaching of quantum mechanics, Am. J. Phys. 70, 537 (2002). [PDF]

Algebraic approach via operator identities

Time-evolution

  • Decompositions of ordered operator exponentials for time-evolution in computational quantum physics
  • M. S. Rudner and N. H. Lindner, The Floquet engineer's handbook, arXiv:2003.08252.
  • R. Merlin, Rabi oscillations, Floquet states, Fermi's golden rule, and all that: Insights from an exactly solvable two-level model, Am. J. Phys. 89, 26 (2021). [PDF]
  • S. Blanes, F. Casas, J. A. Oteo, and J. Ros, A pedagogical approach to the Magnus expansion, Eur. J. Phys. 31, 907 (2010). [PDF]
  • C. J. Eckhardt, G. Passetti, M. Othman, C. Karrasch, F. Cavaliere, M. A. Sentef, and D. M. Kennes, Quantum Floquet engineering with an exactly solvable tight-binding chain in a cavity, Communications Physics 5, 122 (2022). [PDF]

Quantum Optics

  • M. Bina, The coherent interaction between matter and radiation: A tutorial on the Jaynes-Cummings model, Eur. Phys. J. Special Topics 203, 163 (2012). [PDF]
  • 50 years of Jaynes-Cummings physics
  • G. Grynberg, A. Aspect, and Claude Fabre, Introduction to Quantum Optics: From the Semi-classical Approach to Quantized Light (Cambridge University Press, Cambridge, 2010). [PDF]
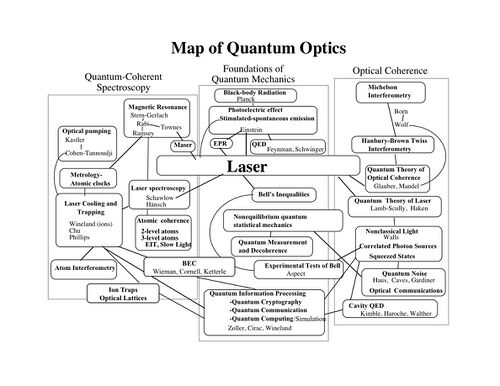
  • Map of Quantum Optics:
Map quantum optics.jpg

Quantum-Classical Methods

  • F. Agostini and B. F. E. Curchod, Different flavors of nonadiabatic molecular dynamics, WIREs Comput. Mol. Sci. 9, e1417 (2019). [PDF]
  • F. Agostini, An exact-factorization perspective on quantum-classical approaches to excited-state dynamics, Euro. Phys. J. B 91, 143 (2018). [PDF]

Quantum Information Science

  • A. Ekert and P. L. Knight, Entangled quantum systems and the Schmidt decomposition, Am. J. Phys. 63, 415 (1995). [PDF]
  • T. Grover, Highly entangled quantum matter [Video]

Open Quantum Systems via Quantum Master Equations

  • P. Pearle, Simple derivation of the Lindblad equation, Eur. J. Phys. 33, 805 (2012). [PDF]
  • D. Manzano, A short introduction to the Lindblad master equation, AIP Adv. 10, 025106 (2020). [PDF]
  • Y. Tanimura, Numerically “exact” approach to open quantum dynamics: The hierarchical equations of motion (HEOM), J. Chem. Phys. 153, 020901 (2020). [PDF]
  • F. Campaioli, J. H. Cole, and H. Hapuarachchi, Tutorial on quantum master equations: Tips and tricks for quantum optics, quantum computing and beyond, arXiv:2303.16449.

Decoherence

  • B. Gu and I. Franco, When can quantum decoherence be mimicked by classical noise?, J. Chem. Phys. 151, 014109 (2019). [PDF]
  • J. Kincaida, K. McLelland, and M. Zwolak, Measurement-induced decoherence and information in double-slit interference, Am. J. Phys. 84, 522 (2016). [PDF]

Quantum Many-Body Systems

Many-body quantum spin systems

  • B. K. Nikolić, From Hubbard dimer to effective antiferromagnetic Hubbard model for two spins
  • B. K. Nikolić, Ground state and low-energy magnon excitations of ferro- and antiferromagnets
  • K. Joel, D. Kollmar, and L. F. Santos, An introduction to the spectrum, symmetries, and dynamics of spin-1/2 Heisenberg chains, Am. J. Phys. 81, 450 (2013). [PDF]
  • F. Mila, Quantum spin liquids, Eur. J. Phys. 21, 499 (2000). [PDF]
  • M. Hoffmann and S. Blügel, Systematic derivation of realistic spin models for beyond-Heisenberg solids, Phys. Rev. B 101, 024418 (2020). [PDF]
  • S. Kitamura, T. Oka, and H. Aoki, Probing and controlling spin chirality in Mott insulators by circularly polarized laser, Phys. Rev. B 96, 014406 (2017). [PDF]
  • A. Szilva, Y. Kvashnin, E. A. Stepanov, O. Eriksson, A. I. Lichtenstein, and M. I. Katsnelson, Quantitative theory of magnetic interactions in solids, Rev. Mod. Phys. 95, 035004 (2023). [PDF]

Computational algorithms

  • G. Catarina and B. Murta, Density-matrix renormalization group: a pedagogical introduction, Eur. Phys. J. B 96, 111 (2023). [PDF]
  • J. Hauschild and F. Pollmann, Efficient numerical simulations with Tensor Networks: Tensor Network Python (TeNPy), SciPost Phys. Lect. Notes 5 (2018). [PDF]

Path Integral

  • D. H. Rischke, "In-out" (or Feynman) path integrals in quantum mechanics [PDF]
  • "In-in" (or Scwinger-Keldysh) path integral formulation of nonequilibrium quantum statistical mechanics [PDF]
  • Y. BenTov, Schwinger-Keldysh path integral for the quantum harmonic oscillator, arXiv:2102.05029

Quantum Field Theory

  • S. Diehl, Lindblad meets Keldysh: Phase transitions, topology, and measurements [PDF]

Numeric and Symbolic Packages

  • SNEG Mathematica package for analytical calculations in second quantization.
  • QuSpin Python package for numerical calculations (exact diagonalization and quantum dynamics) of arbitrary boson, fermion and spin many-body systems.
  • HOQST Julia package for numerical calculations of time evolution of open quantum systems, such as qubits in dissipative environment.
  • QuTiP Python package for numerical calculations of time evolution of open quantum systems, such as qubits in dissipative environment. 
conda config --append channels conda-forge
conda install qutip
Retrieved from "https://wiki.physics.udel.edu/wiki_phys800/index.php?title=Topics&oldid=226"