Homework Set 3: Difference between revisions
| (22 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Problem 1== | ==Problem 1: Energy-momentum dispersion in graphene== | ||
The energy momentum-dispersion of graphene valence and conduction bands is given by the formula derived in class: | |||
<math> E(k_x,k_y) = \pm t\sqrt{1 + 4 \cos \left( \frac{\sqrt{3}}{2} k_x a \right) \cos \left( \frac{k_y a}{2} \right) + 4 \cos^2 \left( \frac{k_y a}{2} \right )} </math> | |||
which assumes tight-binding Hamiltonian projected to a basis set of single <math> \pi </math> orbital per carbon atom and hopping allowed only between the nearest neighbor carbon atoms. The honeycomb lattice spacing is <math> a </math>. | |||
<math> | :'''(a)''' Using MATLAB or Mathematica plot this function as a surface in 3D k-space within the range of <math> (k_x,k_y) </math> vector values defined by the first Brillouin zone. | ||
which | :'''(b)''' Near one of the two inequivalent K points [the so-called Dirac points at which <math> E(k_x,k_y) \equiv 0 </math>] in the corners of the first Brillouin zone, where the conduction (top surface) and valence (bottom surface) bands touch, the dispersion has a conical shape characteristics of massless relativistic particles (such as photons or neutrinos). Up to what energy away from the Dirac point <math> E=0 </math> (which is the Fermi energy of ideal undoped graphene) can the real dispersion shown in your figure be approximated by linear dispersion of the "Dirac cones"? You can subtract <math> E(k_x,k_y) </math> surface around one of the K points from the conical surface <math> E(q_x, q_y) = \pm v_F \hbar \sqrt{q_x^2+q_y^2} </math> (corrections are <math> O[(q/K)]^2</math>; here <math> \mathbf{q} = \mathbf{K} + \mathbf{k} </math> and the Fermi velocity is <math> v_F = \frac{\sqrt{3}}{2} t a/\hbar \approx 10^6 m/s </math>) and find at which energy <math> \pm E_0 </math> their difference starts to be more than 5%. | ||
==Problem 2: Density of state of graphene== | |||
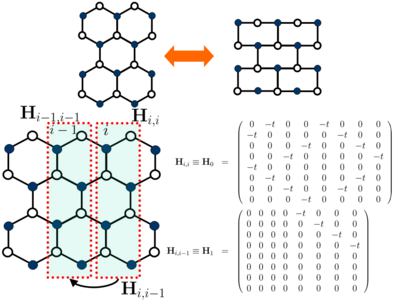
The honeycomb lattice of graphene is topologically equivalent to a brick lattice shown in the Figure below: | |||
[[Image:Graphene_brick.png||thumb|center|400px|Honeycomb lattice of graphene (top left), its equivalent brick lattice (top right) and submatrices of the matrix representation of the tight-binding Hamiltonian defined on either of these two lattices.]] | |||
Thus, the matrix representation of the Hamiltonian defined on this lattice can be obtained in the same fashion as for the square lattice (used in Problem 4. of Homework Set 2), i.e., by loading its submatrices <math> \mathbf{H}_0 </math> describing graphene supercells coupled to adjacent supercells via the hopping submatrices <math> \mathbf{H}_1 </math>. The carbon atoms within the supercells as well as the structure of these submatrices are shown in the Figure. Here it is assumed that electron can hop between only the nearest neighbor carbon atoms with probability <math> t </math>. | |||
( | :'''(a)''' Using the honeycomb (or equivalent brick) lattice of <math> 59 \times 30 </math> carbon atoms (for example, the honeycomb lattice in the top inset of the Figure above is <math> 5 \times 4 </math> in this terminology), construct the full Hamiltonian matrix <math> \mathbf{H} </math> of finite size graphene sheet and compute its density of states (DOS) via the Green function method used in Homework Set 2 in the energy range <math> [-3.5t, 3.5t]</math>. | ||
:'''(b)''' Introduce periodic boundary into <math> \mathbf{H} </math> (this requires to input two additional submatrices <math> \mathbf{H}_1 </math> into <math> \mathbf{H} </math>, as well as to introduce extra hoppings <math> t </math> into <math> \mathbf{H}_0 </math>) and compute its DOS via the same method as in (a). | |||
:'''(c)''' Does any of your numerically obtained DOS for finite-size graphene sheet resembles analytical DOS shown in Fig. 5 (page 114) of A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, ''The electronic properties of graphene'', Rev. Mod. Phys. '''81''', 109 (2009). [http://link.aps.org/doi/10.1103/RevModPhys.81.109 [PDF]]? | |||
'''HINT:''' Test if your Hamiltonian is properly set up with the MATLAB function '''visual_graphene_H.m''' posted on the [[Computing]] page of PHYS 824 wiki. The function will plot real space position of the carbon atoms and the hoppings between them, based on the matrix content and lattice size you supply as an input. | |||
==Problem 3: Massive Dirac particles in graphene== | |||
Consider a tight-binding model on a honeycomb lattice with on-site potential1 different on the sublattices A and B, <math> V_A = - V_B = \lambda </math>. | |||
<math> | : '''(a)''' Develop a general solution of this problem in terms of plane wave states, expressing the spectrum of excitations in terms of the nearest neighbor hopping amplitude <math> t </math> and the asymmetry parameter <math> \Delta = \frac{1}{2} \left(V_A - V_B \right) </math>. | ||
: '''(b)''' Linearize the solution found in part a) near the points <math> K </math> and <math> K^\prime </math> treating the asymmetry as a small perturbation, and find how the massless Dirac picture (valid for <math> V_A = V_B = 0 </math>) of low energy states of graphene is altered. That is, show that <math> \Delta </math> generates a finite mass of Dirac quasiparticles whose Hamiltonian is given by: | |||
<math> \hat{H} = v_F \hat{\mathbf{\sigma}} \cdot \hat{\mathbf{p}} + \lambda \hat{\sigma}_z </math>, | |||
where | where <math> \lambda = V_A = - V_B </math>. | ||
==Problem 4: Bilayer graphene== | |||
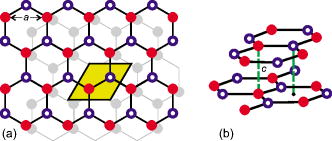
The graphene bilayers are expected to play an important role in nanoelectronic device fabrication since one can manipulate their electronic structure and band gaps (see, e.g., [http://www.nature.com/nmat/journal/v7/n2/abs/nmat2082.html Nature Materials 7, 151 (2007)]] Suppose that two graphene layers are stacked atop one another according to the "Bernal stacking" (the stacking fashion of graphite). This means that the B sublattice sites of the upper layer (layer 1) are directly above the A sublattice sites of the lower layer (layer 2). The A sublattice sites of the upper layer and the B sublattice sites of the lower layer have no "partner" atoms below/above them, as shown in the Figure below. | |||
[[Image:bilayer.jpg||thumb|center|400px|Lattice of bilayer graphene.]] | |||
<math> | :'''(a)''' Formulate and solve the tight-binding model for this system consisting of the usual hopping <math> t </math> between nearest-neighbor sites in each layer, and an additional smaller hopping <math> t_b </math> between the B1-A2 sites in different layers. Choose the zero of energy to equal that of an isolated atom. You should find 4 bands. | ||
:'''(b)''' Two of the bands found above touch at the Fermi energy <math> E_F= 0 </math> at the Brillouin zone boundary points ±K. Find the effective mass around these points. | |||
:'''(c)''' Calculate the Berry phase acquired by an electron encircling one of the zone boundary points in each of the two touching bands. Use your result to argue that the bands cannot split if a small perturbation is applied provided inversion and time-reversal symmetry are preserved. Where is the inversion center for the bilayer? REFERENCE: [http://link.aip.org/link/?LTPHEG/34/794/1 The Berry phase in graphene and graphite multilayers]. | |||
:'''(d)''' ''Check this conclusion in a simple case:'' Because the B1 and A2 sites have more atoms close by than the B2 and A1 sites, there will generally be some difference of the site energies for these orbitals. Add an energy <math> +U_0 </math> to the electrons on the B1, A2 sites and <math> -U_0 </math> to the electrons on the B2, A1 sites. Show that for small enough <math> U_0 </math>, the two bands still touch. | |||
''' | '''REFERENCE:''' B. Partoens and F. M. Peeters, ''From graphene to graphite: Electronic structure around the K point'', Phys. Rev. B '''74''', 075404 (2006). [http://link.aps.org/doi/10.1103/PhysRevB.74.075404 [PDF]] | ||
== Problem 5: Chiral dynamics and Klein tunneling of electrons in graphene== | |||
Consider motion of massless Dirac fermions in an external potential, as described by the Hamiltonian: | |||
<math> \hat{H}_\mathrm{Weyl} = v_F \hat{\mathbf{\sigma}} \cdot \mathbf{p} + U(x) </math> | |||
:'''(a)''' For a rectangular potential barrier, <math> U(x)=V_0, \, 0<x<D </math> and <math> U(x)=0</math> otherwise, find transmission as a function of the incidence angle. | |||
:'''(b)''' For a step-like potential <math> U(x) = U_0 \mathrm{sign}(x) </math> find transmission as a function of the incidence | |||
angle. For simplicity, consider the case of particle at zero Fermi energy (zero doping). | |||
:'''(c)''' What happens at normal incidence <math> k_y = 0 </math> in both (a) and (b)? | |||
'''REFERENCES''' | |||
===Theory=== | |||
*M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, ''Chiral tunnelling and the Klein paradox in graphene'', Nature Physics '''2''', 620 (2006). [http://www.condmat.physics.manchester.ac.uk/pdf/mesoscopic/publications/graphene/Naturephys_2006_Klein.pdf [PDF]] | |||
===Experiment=== | |||
* A. F. Young and P. Kim, ''Quantum interference and Klein tunnelling in graphene heterojunctions'', Nature Phys. '''5''', 222 (2009). [http://www.nature.com/nphys/journal/v5/n3/abs/nphys1198.html [PDF]] | |||
Latest revision as of 13:35, 18 October 2018
Problem 1: Energy-momentum dispersion in graphene
The energy momentum-dispersion of graphene valence and conduction bands is given by the formula derived in class:
which assumes tight-binding Hamiltonian projected to a basis set of single orbital per carbon atom and hopping allowed only between the nearest neighbor carbon atoms. The honeycomb lattice spacing is .
- (a) Using MATLAB or Mathematica plot this function as a surface in 3D k-space within the range of vector values defined by the first Brillouin zone.
- (b) Near one of the two inequivalent K points [the so-called Dirac points at which Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(k_x,k_y) \equiv 0 } ] in the corners of the first Brillouin zone, where the conduction (top surface) and valence (bottom surface) bands touch, the dispersion has a conical shape characteristics of massless relativistic particles (such as photons or neutrinos). Up to what energy away from the Dirac point Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E=0 } (which is the Fermi energy of ideal undoped graphene) can the real dispersion shown in your figure be approximated by linear dispersion of the "Dirac cones"? You can subtract Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(k_x,k_y) } surface around one of the K points from the conical surface Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(q_x, q_y) = \pm v_F \hbar \sqrt{q_x^2+q_y^2} } (corrections are Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O[(q/K)]^2} ; here Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{q} = \mathbf{K} + \mathbf{k} } and the Fermi velocity is Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_F = \frac{\sqrt{3}}{2} t a/\hbar \approx 10^6 m/s } ) and find at which energy Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pm E_0 } their difference starts to be more than 5%.
Problem 2: Density of state of graphene
The honeycomb lattice of graphene is topologically equivalent to a brick lattice shown in the Figure below:
Thus, the matrix representation of the Hamiltonian defined on this lattice can be obtained in the same fashion as for the square lattice (used in Problem 4. of Homework Set 2), i.e., by loading its submatrices Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_0 }
describing graphene supercells coupled to adjacent supercells via the hopping submatrices Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_1 }
. The carbon atoms within the supercells as well as the structure of these submatrices are shown in the Figure. Here it is assumed that electron can hop between only the nearest neighbor carbon atoms with probability Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t }
.
- (a) Using the honeycomb (or equivalent brick) lattice of Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 59 \times 30 } carbon atoms (for example, the honeycomb lattice in the top inset of the Figure above is Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5 \times 4 } in this terminology), construct the full Hamiltonian matrix Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} } of finite size graphene sheet and compute its density of states (DOS) via the Green function method used in Homework Set 2 in the energy range Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [-3.5t, 3.5t]} .
- (b) Introduce periodic boundary into Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} } (this requires to input two additional submatrices Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_1 } into Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} } , as well as to introduce extra hoppings Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t } into Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_0 } ) and compute its DOS via the same method as in (a).
- (c) Does any of your numerically obtained DOS for finite-size graphene sheet resembles analytical DOS shown in Fig. 5 (page 114) of A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys. 81, 109 (2009). [PDF]?
HINT: Test if your Hamiltonian is properly set up with the MATLAB function visual_graphene_H.m posted on the Computing page of PHYS 824 wiki. The function will plot real space position of the carbon atoms and the hoppings between them, based on the matrix content and lattice size you supply as an input.
Problem 3: Massive Dirac particles in graphene
Consider a tight-binding model on a honeycomb lattice with on-site potential1 different on the sublattices A and B, Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_A = - V_B = \lambda } .
- (a) Develop a general solution of this problem in terms of plane wave states, expressing the spectrum of excitations in terms of the nearest neighbor hopping amplitude Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t } and the asymmetry parameter Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta = \frac{1}{2} \left(V_A - V_B \right) } .
- (b) Linearize the solution found in part a) near the points Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K } and Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K^\prime } treating the asymmetry as a small perturbation, and find how the massless Dirac picture (valid for Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_A = V_B = 0 } ) of low energy states of graphene is altered. That is, show that Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta } generates a finite mass of Dirac quasiparticles whose Hamiltonian is given by:
Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \hat{H} = v_F \hat{\mathbf{\sigma}} \cdot \hat{\mathbf{p}} + \lambda \hat{\sigma}_z }
,
where Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda = V_A = - V_B }
.
Problem 4: Bilayer graphene
The graphene bilayers are expected to play an important role in nanoelectronic device fabrication since one can manipulate their electronic structure and band gaps (see, e.g., Nature Materials 7, 151 (2007)] Suppose that two graphene layers are stacked atop one another according to the "Bernal stacking" (the stacking fashion of graphite). This means that the B sublattice sites of the upper layer (layer 1) are directly above the A sublattice sites of the lower layer (layer 2). The A sublattice sites of the upper layer and the B sublattice sites of the lower layer have no "partner" atoms below/above them, as shown in the Figure below.
- (a) Formulate and solve the tight-binding model for this system consisting of the usual hopping Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t } between nearest-neighbor sites in each layer, and an additional smaller hopping Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t_b } between the B1-A2 sites in different layers. Choose the zero of energy to equal that of an isolated atom. You should find 4 bands.
- (b) Two of the bands found above touch at the Fermi energy Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E_F= 0 } at the Brillouin zone boundary points ±K. Find the effective mass around these points.
- (c) Calculate the Berry phase acquired by an electron encircling one of the zone boundary points in each of the two touching bands. Use your result to argue that the bands cannot split if a small perturbation is applied provided inversion and time-reversal symmetry are preserved. Where is the inversion center for the bilayer? REFERENCE: The Berry phase in graphene and graphite multilayers.
- (d) Check this conclusion in a simple case: Because the B1 and A2 sites have more atoms close by than the B2 and A1 sites, there will generally be some difference of the site energies for these orbitals. Add an energy Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle +U_0 } to the electrons on the B1, A2 sites and Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -U_0 } to the electrons on the B2, A1 sites. Show that for small enough Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U_0 } , the two bands still touch.
REFERENCE: B. Partoens and F. M. Peeters, From graphene to graphite: Electronic structure around the K point, Phys. Rev. B 74, 075404 (2006). [PDF]
Problem 5: Chiral dynamics and Klein tunneling of electrons in graphene
Consider motion of massless Dirac fermions in an external potential, as described by the Hamiltonian:
Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \hat{H}_\mathrm{Weyl} = v_F \hat{\mathbf{\sigma}} \cdot \mathbf{p} + U(x) }
- (a) For a rectangular potential barrier, Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U(x)=V_0, \, 0<x<D } and Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U(x)=0} otherwise, find transmission as a function of the incidence angle.
- (b) For a step-like potential Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U(x) = U_0 \mathrm{sign}(x) } find transmission as a function of the incidence
angle. For simplicity, consider the case of particle at zero Fermi energy (zero doping).
- (c) What happens at normal incidence Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k_y = 0 } in both (a) and (b)?
REFERENCES
Theory
- M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, Chiral tunnelling and the Klein paradox in graphene, Nature Physics 2, 620 (2006). [PDF]
Experiment
- A. F. Young and P. Kim, Quantum interference and Klein tunnelling in graphene heterojunctions, Nature Phys. 5, 222 (2009). [PDF]