Homework Set 4: Difference between revisions

From phys824
Jump to navigationJump to search
No edit summary
 
(37 intermediate revisions by the same user not shown)
Line 1: Line 1:
'''Pick problem 1 and three other problems among 2,3,4,5, and 6. Students who try to solve all six problems will be given extra credit.'''
==Problem 1==
==Problem 1==
The energy momentum-dispersion of graphene valence and conduction bands is given by the formula derived in class:


The two-dimensional electron gas (2DEG) in semiconductor heterostructures with structural inversion asymmetry in the growth direction (perpendicular to the 2DEG plane) plays an essential role in the pursuit of [http://physics.aps.org/articles/v2/50 "spintronics without magnetism"] since the spin of an electron in nanostructures made of such 2DEGs can be controlled by electrical fields (which can be controlled on much smaller spatial and temporal scales than traditional cumbersome magnetic fields). Such control is made possible by the spin-orbit (SO) couplings which represent manifestations of relativistic quantum mechanics in solids (enhanced, when compared to corrections in vacuum, by the band structure effects). 
<math> E(k_x,k_y) = \pm t\sqrt{1 + 4 \cos \left( \frac{\sqrt{3}}{2} k_x a \right) \cos \left( \frac{k_y a}{2} \right) + 4 \cos^2 \left( \frac{k_y a}{2} \right )} </math>
 
The important SO coupling for 2DEGs are the linear Rashba and Dresselhaus ones, encoded by the following effective mass Hamiltonian:
 
<math> \hat{H}  = \frac{\hat{p}_x^2 + \hat{p}_y^2}{2 m^*} + \frac{\alpha}{\hbar} \left( \hat{p}_y \hat{\sigma}_x  - \hat{p}_x  \hat{\sigma}_y  \right) +
\frac{\beta}{\hbar} \left(\hat{p}_x \hat{\sigma}_x  - \hat{p}_y \hat{\sigma}_y  \right) </math>, (1)
 
where <math> \alpha </math> measures the strength of the Rashba coupling and <math> \beta </math> measures the strength of the Dresselhaus coupling. Here <math> (\hat{p}_x,\hat{p}_y) </math> is the two-dimensional momentum operator and <math> \mathbf{\sigma} = (\sigma_x,\sigma_y,\sigma_z) </math> is the vector of Pauli spin matrices. In GaAs quantum wells the two terms are of the same order of magnitude, while the Rashba SO coupling dominates in narrow band-gap InAs-based structures [the relative strength  <math> \alpha/\beta </math> can be extracted from, e.g., photocurrent measurements, [http://prola.aps.org/abstract/PRL/v92/i25/e256601 Phys. Rev. Lett. '''92''', 256601 (2004)]].
 
 
a) Assume a toy model of 1DEG with the Rashba coupling described by the Hamiltonian:
 
<math> \hat{H}^{\rm 1D}_{\rm R}(k_x)=\frac{\hbar^2k_x^2}{2m^*}-\alpha k_x\hat{\sigma}_y </math>
 
Find its eigenstates and eigenvalues as a function of <math> k_x </math>. Using Mathematics or Matlab, plot both branches of <math> E(k_x) </math>.
 
b) For the Rashba-dominated 2DEG, <math> \alpha > 0 </math>, <math> \beta = 0 </math>, find eigenstates and eigenvalues of the Hamiltonian (1) and use Mathematica or Matlab to plot the corresponding <math> E(k_x,k_y) </math> dispersion surface.
 
c) What is the expectation value <math> \langle \Psi_{\pm}(\mathbf{k}) |\hbar \mathbf{\sigma}/2| \Psi_{\pm}(\mathbf{k}) \rangle </math> of the spin operator <math> \hbar \mathbf{\sigma}/2 </math> in the eigenstates of spin-split 1DEG in a) and spin-split 2DEG in b)?


d) For <math> \alpha = \beta </math> in the Hamiltonian (1), a spin-helix state of 2DEG can be generated [recently confirmed experimentally, [http://www.nature.com/nature/journal/v458/n7238/full/nature07871.html Nature '''458''', 610 (2009)]] within which spins become immune to relaxation. Transform such Hamiltonian into the diagonal form given by Eq. (2) in [http://link.aps.org/doi/10.1103/PhysRevLett.100.236601 Phys. Rev. Lett. '''97''', 236601 (2006)], and write explicitly its eigenvalues and eigestates.
which assumes tight-binding Hamiltonian projected to a basis set of single <math> \pi </math> orbital per carbon atom and hopping allowed only between the nearest neighbor carbon atoms. The honeycomb lattice spacing is <math> a </math>.


:'''(a)''' Using MATLAB or Mathematica plot this function as a surface in 3D k-space within the range of <math> (k_x,k_y) </math> vector values defined by the first Brillouin zone.


REFERENCE: B. K. Nikolic, L. P. Zarbo, and S. Souma, [http://www.physics.udel.edu/~bnikolic/PDF/spin_currents_oup.pdf ''Spin currents in semiconductor nanostructures: A nonequilibrium Green-function approach''], Chapter 24 in Volume I of "The Oxford Handbook on Nanoscience and Technology: Frontiers and Advances" (Oxford University Press, Oxford, 2010).
:'''(b)''' Near one of the two inequivalent K points [the so-called Dirac points at which <math> E(k_x,k_y) \equiv 0 </math>] in the corners of the  first Brillouin zone, where the conduction (top surface) and valence (bottom surface) bands touch, the dispersion has a conical shape characteristics of massless relativistic particles (such as photons or neutrinos). Up to what energy away from the Dirac point <math> E=0 </math> (which is the Fermi energy of ideal undoped graphene) can the real dispersion shown in your figure be approximated by linear dispersion of the "Dirac cones"? You can subtract <math> E(k_x,k_y) </math> surface around one of the K points from the conical surface <math> E(q_x, q_y) = \pm v_F \hbar \sqrt{q_x^2+q_y^2} </math> (corrections are <math> O[(q/K)]^2</math>; here <math> \mathbf{q} = \mathbf{K} + \mathbf{k} </math> and the Fermi velocity is <math> v_F = \frac{\sqrt{3}}{2} t a/\hbar \approx 10^6 m/s </math>) and find at which energy <math> \pm E_0 </math> their difference starts to be more than 5%.


==Problem 2==
==Problem 2==


'''Magnetoelectric effect:''' The spin accumulation in 2DEG described by the Rashba spin-split Hamiltonian (1), with <math> \alpha \neq 0 </math> and <math> \beta =0 </math>, is zero in equilibrium since SO coupling does not break the time-reversal invariance and spin changes it sign under such operation (therefore, since <math> \mathbf{S}=-\mathbf{S} </math> in time-reversal invariant systems, <math> \mathbf{S} \equiv 0 </math>). The non-zero spin accumulation within the Rashba-coupled 2DEG can be generated by the application of in-plane electric field [as confirmed in the recent experiments, e.g., [http://dx.doi.org/10.1016/j.jmmm.2005.10.048 Journal of Magnetism and Magnetic Materials '''300''', 127 (2006)]].
The honeycomb lattice of graphene is topologically equivalent to a brick lattice shown in the Figure below:
 
Find the relation between <math> \langle \mathbf{S} \rangle </math> and the applied electric field <math> \mathbf{E}=(E_x,E_y) </math> in the xy-plane of the 2DEG by using equation for spin density in 2D:
 
<math> \langle \mathbf{S} \rangle = \int \frac{d^2 \mathbf{k}}{(2\pi)^2}  f(\mathbf{k}) \langle \Psi^{\pm}_\mathbf{k} |\hbar \mathbf{\sigma}/2| \Psi^{\pm}_\mathbf{k} \rangle </math>,
 
that is analogous (i.e., density of states X the filling factor for each state X the value of the physical quantity in each state) to the equation for electron density introduced at the beginning of the PHYS824 course.
 
The nonequilibrium distribution function in the linear response approximation (i.e., to first order in the electric field) is given by:


<math> f_{\pm} (\mathbf{k}) = f_0 (\varepsilon_{\mathbf{k}}) + \tau f'(\varepsilon_{\mathbf{k}}) \mathbf{E} \cdot  \nabla \varepsilon_{\pm} (\mathbf{k}) </math>,
[[Image:Graphene_brick.png||thumb|center|400px|Honeycomb lattice of graphene (top left), its equivalent brick lattice (top right) and submatrices of the matrix representation of the tight-binding Hamiltonian defined on either of these two lattices.]]


for either of the two <math> \pm </math> spin-split bands found in Problem 1:


<math> \hat{H}_\mathrm{Rashba} |\Psi^{\pm}_\mathbf{k} \rangle = \varepsilon_{\pm}(\mathbf{k}) |\Psi^{\pm}_\mathbf{k} \rangle </math>.
Thus, the matrix representation of the Hamiltonian defined on this lattice can be obtained in the same fashion as for the square lattice (used in Problem 4. of Homework Set 2), i.e., by loading its submatrices <math> \mathbf{H}_0 </math> describing graphene supercells coupled to adjacent supercells via the hopping submatrices <math> \mathbf{H}_1 </math>. The carbon atoms within the supercells as well as the structure of these submatrices are shown in the Figure. Here it is assumed that electron can hop between only the nearest neighbor carbon atoms with probability <math> t </math>.  


Here <math> f_0 (\varepsilon_{\mathbf{k}}) </math> is the equilibrium Fermi-Dirac distribution function and <math> \tau </math> is the mean-free time.
:'''(a)''' Using the honeycomb (or equivalent brick) lattice of <math> 59 \times 30 </math> carbon atoms (for example, the honeycomb lattice in the top inset of the Figure above is <math> 5 \times 4 </math> in this terminology), construct the full Hamiltonian matrix <math> \mathbf{H} </math> of finite size graphene sheet and compute its density of states (DOS) via the Green function method used in Homework Set 2 in the energy range <math> [-3.5t, 3.5t]</math>.  


NOTE: This means that the general expression for the bulk spin density above reduces in this case to a sum of two terms:
:'''(b)''' Introduce periodic boundary into <math> \mathbf{H} </math> (this requires to input two additional submatrices <math> \mathbf{H}_1 </math> into <math> \mathbf{H} </math>, as well as to introduce extra hoppings <math> t </math> into <math> \mathbf{H}_0 </math>) and compute its DOS via the same method as in (a).


<math> \langle \mathbf{S} \rangle = \int \frac{d^2 \mathbf{k}}{(2\pi)^2} f_{+}(\mathbf{k}) \langle \Psi^+_\mathbf{k} |\hbar \mathbf{\sigma}/2| \Psi^{+}_\mathbf{k} \rangle + \int \frac{d^2 \mathbf{k}}{(2\pi)^2} f_{-}(\mathbf{k})  \langle \Psi^-_\mathbf{k} |\hbar \mathbf{\sigma}/2| \Psi^{-}_\mathbf{k} \rangle </math>.
:'''(c)''' Does any of your numerically obtained DOS for finite-size graphene sheet resembles analytical DOS shown in Fig. 5 (page 114) of A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, ''The electronic properties of graphene'', Rev. Mod. Phys. '''81''', 109 (2009). [http://link.aps.org/doi/10.1103/RevModPhys.81.109 [PDF]]?


You can test correctness of your expression by checking that it goes to zero for vanishing SO coupling <math> \alpha \rightarrow 0 </math>.
'''HINT:''' Test if your Hamiltonian is properly set up with the MATLAB function '''visual_graphene_H.m''' posted on the [[Computing]] page of PHYS 824 wiki. The function  will plot real space position of the carbon atoms and the hoppings between them, based on the matrix content and lattice size you supply as an input.


==Problem 3==
==Problem 3==


[[Image:cpc.png||thumb|left|400px|Model of a classical point contact between two massive metallic electrodes.]]
'''Massive Dirac particles in graphene:''' Consider a tight-binding model on a honeycomb lattice with on-site potential1 different on the sublattices A and B, <math> V_A = - V_B = \lambda </math>.


'''Classical point contact conductance:''' The Sharvin formula for the electrical conductance of an extremely short contact area <math> A </math> between two pieces of metal is given by
: '''(a)''' Develop a general solution of this problem in terms of plane wave states, expressing the spectrum of excitations in terms of the nearest neighbor hopping amplitude <math> t </math> and the asymmetry parameter <math> \Delta  = \frac{1}{2} \left(V_A - V_B \right) </math>.


<math> G=\frac{2e^2}{h}\frac{k_F^2 A}{4\pi} </math>
: '''(b)''' Linearize the solution found in part a) near the points <math> K </math> and <math> K^\prime </math> treating the asymmetry  as a small perturbation, and find how the massless Dirac picture (valid for <math> V_A = V_B = 0 </math>) of low energy states of graphene  is altered. That is, show that <math> \Delta </math> generates a finite mass of Dirac quasiparticles whose Hamiltonian is given by:


where <math> k_F </math> is the Fermi wavelength. Derive the Sharvin formula by considering the total current flowing through a hole of area $A$ in a thin insulating barrier separating two free electron gases with different Fermi energies, as shown in the Figure above. The gas on the left has Fermi energy $E_F + eV$, while the gas on the right has Fermi energy $\varepsilon_F^0$, where $V$ is the applied voltage bias.


Use purely macroscopic arguments:
<math> \hat{H} = v_F \hat{\mathbf{\sigma}} \cdot \hat{\mathbf{p}}  + \lambda \hat{\sigma}_z </math>,


1) The total current through the contact is


<math> I = j_z A </math>
where <math> \lambda = V_A = - V_B </math>.


where current density along the z-axis is (carried by electrons within the bias window <math> E_F </math> to <math> E_F+eV </math>):
==Problem 4==


<math> j_z = \int_{E_F}^{E_F+eV} dE\, \int d\theta v_z \frac{\partial^2 n}{\partial E \partial \theta} </math>.
'''Bilayer graphene:''' The graphene bilayers are expected to play an important role in nanoelectronic device fabrication since one can manipulate their electronic structure and band gaps (see, e.g., [http://www.nature.com/nmat/journal/v7/n2/abs/nmat2082.html Nature Materials 7, 151 (2007)]] Suppose that two graphene layers are stacked atop one another according to the "Bernal stacking" (the stacking fashion of graphite). This means that the B sublattice sites of the upper layer (layer 1) are directly above the A sublattice sites of the lower layer (layer 2). The A sublattice sites of the upper layer and the B sublattice sites of the lower layer have no "partner" atoms below/above them, as shown in the Figure below.


[[Image:bilayer.jpg||thumb|center|400px|Lattice of bilayer graphene.]]


2) In a free electron gas, the number of electrons with energies between <math> E </math> and <math> E+dE </math> traveling at an angle between <math>\theta</math> and <math>\theta + d\theta</math> with respect to a given axis is
:'''(a)''' Formulate and solve the tight-binding model for this system consisting of the usual hopping <math> t </math> between nearest-neighbor sites in each layer, and an additional smaller hopping <math> t_b </math> between the B1-A2 sites in different layers. Choose the zero of energy to equal that  of an isolated atom. You should find 4 bands.


<math> \frac{\partial^2 n}{\partial E \partial \theta} dE d\theta = \frac{g(E)}{2} \sin \theta dE d\theta </math>,
:'''(b)''' Two of the bands found above touch at the Fermi energy <math> E_F= 0 </math> at the Brillouin zone boundary points ±K. Find the effective mass around these points.


where <math> g(E) </math> is the density of states in three dimensions.
:'''(c)''' Calculate the Berry phase acquired by an electron encircling one of the zone boundary points in each of the two touching bands. Use your result to argue that the bands cannot split if a small perturbation is applied provided inversion and time-reversal symmetry are preserved. Where is the inversion center for the bilayer? REFERENCE: [http://link.aip.org/link/?LTPHEG/34/794/1 The Berry phase in graphene and graphite multilayers].


==Problem 4==
:'''(d)''' ''Check this conclusion in a simple case:'' Because the B1 and A2 sites have more atoms close by than the B2 and A1 sites, there will generally be some difference of the site energies for these orbitals. Add an energy <math> +U_0 </math> to the electrons on the B1, A2 sites and <math> -U_0 </math> to the electrons on the B2, A1 sites. Show that for small enough <math> U_0 </math>, the two bands still touch.


'''Quantum point contact conductance:''' When the size of the contact from Problem 3 becomes comparable to the Fermi wavelength <math> \lambda_F = 2\pi/k_F </math>, the contact enters the quantum regime where its conductance becomes quantized as defined by the Landauer formula:
'''REFERENCE:''' B. Partoens and F. M. Peeters, ''From graphene to graphite: Electronic structure around the K point'', Phys. Rev. B '''74''', 075404 (2006). [http://link.aps.org/doi/10.1103/PhysRevB.74.075404 [PDF]]
 
<math> G = \frac{2e^2}{h} \sum_{n=1}^N T_n = N </math>.
 
Here <math> N </math> is the number of "conducting channels" assumed to have perfect transmission <math> T_n =1 </math> in ballistic transport at zero temperture. One can also view the Sharvin formula from Problem 3 as a limiting case of such Landauer formula where the number of channels
<math> N_{\mathrm{classical}} = \frac{k_F^2 A}{4 \pi} </math> (in three dimensions) is very large, so that <math> N_{\mathrm{classical}}</math> is a continuous function of <math> k_F </math> (rather than discrete <math> N </math> in the Landauer formula above).
 
Find resistance in Ohm of such contact modeled by a two-dimensional wire (joining the macroscopic reservoirs) in the form of a strip of width <math> W = 1.75 \lambda_F </math>. Assume that conduction electrons in the wire can be described by the free-particle Schrodinger equation with hard-wall [i.e., <math> \Psi(\mathbf{r})=0 </math>] boundary conditions along the lateral edges of the strip.


== Problem 5 ==
== Problem 5 ==
'''Chiral dynamics and Klein tunneling of low-energy quasiparticles in graphene:''' Consider motion of massless Dirac fermions in an external potential, as described by the Hamiltonian:


Suppose that a quantum wire can be modeled by a 2D strip with hard-wall boundary conditions in the direction transverse to the current flow. The width of the wire is 10 nm and the effective mass of electrons is <math> m^* = 0.067m_0 </math> of the bare electron mass <math> m_0 </math> (which is the case for GaAs heterostructures).
<math> \hat{H}_\mathrm{Weyl} = v_F \hat{\mathbf{\sigma}} \cdot \mathbf{p} + U(x) </math>
 
a) Plot the conductance of such a wire as function of the Fermi energy for a number of temperatures <math> T < E_F </math>. The Landauer formula for conductance at finite temperature is:
 
<math> G = \frac{2e^2}{h} \sum_{n=1}^N \left(-\frac{\partial f }{\partial E} \right) T_n(E) </math>


where <math> f(E) </math> is the Fermi-Dirac distribution function and <math> T_n(E) = \theta (E-E_n) </math> [<math> \theta(x) </math> is the step function] since in ballistic wires a channel is either open (when the Fermi energy is above the bottom of the corresponding subband) or closed (otherwise).
:'''(a)''' For a rectangular potential barrier, <math> U(x)=V_0, \, 0<x<D </math> and <math> U(x)=0</math> otherwise, find transmission as a function of the incidence angle.


:'''(b)''' For a step-like potential <math> U(x) = U_0 sign(x) </math> find transmission as a function of the incidence
angle. For simplicity, consider the case of particle at zero Fermi energy (zero doping).


b) Determine characteristic temperature(s) at which features of the quantization plateaux begin to disappear. For simplicity, you can consider only the first two subbands (i.e., conducting channels), <math> n=1,2 </math>.
:'''(c)''' What happens at normal incidence <math> k_y = 0 </math> in both (a) and (b)?


== Problem 6 ==
'''REFERENCES'''


[[Image:2qpc.png||thumb|left|400px|Illustration of the two quantum point contacts in series setup.]]
===Theory===
*M. I. Katsnelson, K. S. Novoselov,  and A. K. Geim, ''Chiral tunnelling and the Klein paradox in graphene'', Nature Physics '''2''', 620 (2006). [http://www.condmat.physics.manchester.ac.uk/pdf/mesoscopic/publications/graphene/Naturephys_2006_Klein.pdf [PDF]]


'''Two quantum point contacts in series:''' Two ballistic quantum point contacts are connected in series, as shown in the Figure below. When measured independently, the conductance of the first contact is <math> \frac{2e^2}{h} </math> and that of the second one is <math> \frac{4e^2}{h} </math>. The whole structure is still ballistic. What is the conductance of the whole structure?
===Experiment===
* A. F. Young and P. Kim, ''Quantum interference and Klein tunnelling in graphene heterojunctions'', Nature Phys. '''5''', 222 (2009). [http://www.nature.com/nphys/journal/v5/n3/abs/nphys1198.html [PDF]]

Latest revision as of 09:23, 24 October 2016

Problem 1

The energy momentum-dispersion of graphene valence and conduction bands is given by the formula derived in class:

which assumes tight-binding Hamiltonian projected to a basis set of single orbital per carbon atom and hopping allowed only between the nearest neighbor carbon atoms. The honeycomb lattice spacing is .

(a) Using MATLAB or Mathematica plot this function as a surface in 3D k-space within the range of vector values defined by the first Brillouin zone.
(b) Near one of the two inequivalent K points [the so-called Dirac points at which ] in the corners of the first Brillouin zone, where the conduction (top surface) and valence (bottom surface) bands touch, the dispersion has a conical shape characteristics of massless relativistic particles (such as photons or neutrinos). Up to what energy away from the Dirac point (which is the Fermi energy of ideal undoped graphene) can the real dispersion shown in your figure be approximated by linear dispersion of the "Dirac cones"? You can subtract surface around one of the K points from the conical surface (corrections are ; here and the Fermi velocity is ) and find at which energy their difference starts to be more than 5%.

Problem 2

The honeycomb lattice of graphene is topologically equivalent to a brick lattice shown in the Figure below:

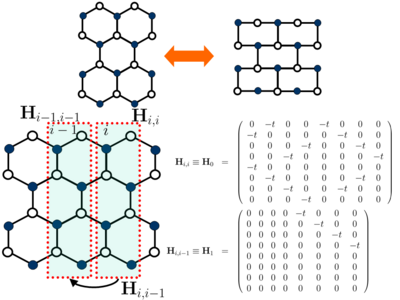
Honeycomb lattice of graphene (top left), its equivalent brick lattice (top right) and submatrices of the matrix representation of the tight-binding Hamiltonian defined on either of these two lattices.


Thus, the matrix representation of the Hamiltonian defined on this lattice can be obtained in the same fashion as for the square lattice (used in Problem 4. of Homework Set 2), i.e., by loading its submatrices describing graphene supercells coupled to adjacent supercells via the hopping submatrices . The carbon atoms within the supercells as well as the structure of these submatrices are shown in the Figure. Here it is assumed that electron can hop between only the nearest neighbor carbon atoms with probability .

(a) Using the honeycomb (or equivalent brick) lattice of carbon atoms (for example, the honeycomb lattice in the top inset of the Figure above is in this terminology), construct the full Hamiltonian matrix of finite size graphene sheet and compute its density of states (DOS) via the Green function method used in Homework Set 2 in the energy range .
(b) Introduce periodic boundary into (this requires to input two additional submatrices into , as well as to introduce extra hoppings into ) and compute its DOS via the same method as in (a).
(c) Does any of your numerically obtained DOS for finite-size graphene sheet resembles analytical DOS shown in Fig. 5 (page 114) of A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys. 81, 109 (2009). [PDF]?

HINT: Test if your Hamiltonian is properly set up with the MATLAB function visual_graphene_H.m posted on the Computing page of PHYS 824 wiki. The function will plot real space position of the carbon atoms and the hoppings between them, based on the matrix content and lattice size you supply as an input.

Problem 3

Massive Dirac particles in graphene: Consider a tight-binding model on a honeycomb lattice with on-site potential1 different on the sublattices A and B, .

(a) Develop a general solution of this problem in terms of plane wave states, expressing the spectrum of excitations in terms of the nearest neighbor hopping amplitude and the asymmetry parameter .
(b) Linearize the solution found in part a) near the points and treating the asymmetry as a small perturbation, and find how the massless Dirac picture (valid for ) of low energy states of graphene is altered. That is, show that generates a finite mass of Dirac quasiparticles whose Hamiltonian is given by:


,


where .

Problem 4

Bilayer graphene: The graphene bilayers are expected to play an important role in nanoelectronic device fabrication since one can manipulate their electronic structure and band gaps (see, e.g., Nature Materials 7, 151 (2007)] Suppose that two graphene layers are stacked atop one another according to the "Bernal stacking" (the stacking fashion of graphite). This means that the B sublattice sites of the upper layer (layer 1) are directly above the A sublattice sites of the lower layer (layer 2). The A sublattice sites of the upper layer and the B sublattice sites of the lower layer have no "partner" atoms below/above them, as shown in the Figure below.

Lattice of bilayer graphene.
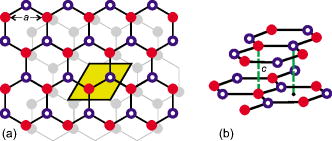
(a) Formulate and solve the tight-binding model for this system consisting of the usual hopping between nearest-neighbor sites in each layer, and an additional smaller hopping between the B1-A2 sites in different layers. Choose the zero of energy to equal that of an isolated atom. You should find 4 bands.
(b) Two of the bands found above touch at the Fermi energy at the Brillouin zone boundary points ±K. Find the effective mass around these points.
(c) Calculate the Berry phase acquired by an electron encircling one of the zone boundary points in each of the two touching bands. Use your result to argue that the bands cannot split if a small perturbation is applied provided inversion and time-reversal symmetry are preserved. Where is the inversion center for the bilayer? REFERENCE: The Berry phase in graphene and graphite multilayers.
(d) Check this conclusion in a simple case: Because the B1 and A2 sites have more atoms close by than the B2 and A1 sites, there will generally be some difference of the site energies for these orbitals. Add an energy to the electrons on the B1, A2 sites and to the electrons on the B2, A1 sites. Show that for small enough , the two bands still touch.

REFERENCE: B. Partoens and F. M. Peeters, From graphene to graphite: Electronic structure around the K point, Phys. Rev. B 74, 075404 (2006). [PDF]

Problem 5

Chiral dynamics and Klein tunneling of low-energy quasiparticles in graphene: Consider motion of massless Dirac fermions in an external potential, as described by the Hamiltonian:

(a) For a rectangular potential barrier, and otherwise, find transmission as a function of the incidence angle.
(b) For a step-like potential find transmission as a function of the incidence

angle. For simplicity, consider the case of particle at zero Fermi energy (zero doping).

(c) What happens at normal incidence in both (a) and (b)?

REFERENCES

Theory

  • M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, Chiral tunnelling and the Klein paradox in graphene, Nature Physics 2, 620 (2006). [PDF]

Experiment

  • A. F. Young and P. Kim, Quantum interference and Klein tunnelling in graphene heterojunctions, Nature Phys. 5, 222 (2009). [PDF]
Retrieved from "https://wiki.physics.udel.edu/wiki_phys824/index.php?title=Homework_Set_4&oldid=2325"