Homework Set 3: Difference between revisions
Blanked the page |
No edit summary |
||
| Line 1: | Line 1: | ||
==Problem 1== | |||
[[Image:sdh.png||thumb|left|400px|Shubnikov-de Haas oscillations in the longitudinal voltage.]] | |||
'''Shubnikov-de Haas oscillations in 2DEG:''' The physical properties of a 2DEG can be measured by embedding it into a multiterminal Hall bridge, as shown in the Figure above. The energy spectrum of 2D electrons in magnetic field <math> \mathbf{B}=B\hat{z} </math> orthogonal to such bridge consists of discrete Landau lavels: | |||
<math> E_n=\hbar \omega \left(n + \frac{1}{2} \right), \ \omega=eB/m^* </math>, | |||
which are well-separated for large enough B. Thus, the step-like density of states associated with 2DEG <math> g(E) = \frac{m^*}{\pi \hbar^2} \theta(E-E_b) </math> (<math> E_b </math> is the lowest level in the triangular potential that confines 2DEG) is then broken up into a series of peaks spaced by <math> \hbar \omega </math>: | |||
<math> g(E,B) = \frac{2eB}{h} \sum_{n=0}^{\infty} \delta \left[ E- E_b - \hbar \omega \left(n + \frac{1}{2} \right)\right] </math>. (1) | |||
Although the spikes are ideally delta functions, scattering processes spread them out in energy. As one changes the magnetic field B, longitudinal voltage (from which one computes the longitudinal resisitivity <math> \rho_{xx}=V_x W/ I L </math>) in the Figure above goes through one cycle of oscillations as the Fermi energy moves from the center of one Landau level to the center of the next Landau level. These oscillations are refered to as the ''Shubnikov-de Haas'' (SdH) oscillations. | |||
(a) Devise a procedure that will allow you to extract electron density <math> n </math> in 2DEG from the values of magnetic field B at which <math> V_x </math> (or the corresponding <math> \rho_{xx} </math>) reaches maximum in the course of SdH oscillations. | |||
(b) What is <math> n </math> for the 2DEG in the Figure above? | |||
HINT: From Eq. (1) we see that the number of occupied Landau levels is <math> n/(2eB/h) </math>, if electron density <math> n </math> is already known. | |||
==Problem 2== | |||
[[Image:cpc.png||thumb|left|400px|Model of a classical point contact between two massive metallic electrodes.]] | |||
'''Classical point contact conductance:''' The Sharvin formula for the electrical conductance of an extremely short contact area <math> A </math> between two pieces of metal is given by | |||
<math> G=\frac{2e^2}{h}\frac{k_F^2 A}{4\pi} </math> | |||
where <math> k_F </math> is the Fermi wavelength. Derive the Sharvin formula by considering the total current flowing through a hole of area <math> A </math> in a thin insulating barrier separating two free electron gases with different Fermi energies, as shown in the Figure above. The gas on the left has Fermi energy <math> E_F + eV </math>, while the gas on the right has Fermi energy <math> \varepsilon_F^0 </math>, where <math> V </math> is the applied voltage bias. | |||
Use purely macroscopic arguments: | |||
1) The total current through the contact is | |||
<math> I = j_z A </math> | |||
where current density along the z-axis is (carried by electrons within the bias window <math> E_F </math> to <math> E_F+eV </math>): | |||
<math> j_z = e\int_{E_F}^{E_F+eV} dE\, \int d\theta v_z \frac{\partial^2 n}{\partial E \partial \theta} </math>. | |||
2) In a free electron gas, the number of electrons with energies between <math> E </math> and <math> E+dE </math> traveling at an angle between <math>\theta</math> and <math>\theta + d\theta</math> with respect to a given axis is | |||
<math> \frac{\partial^2 n}{\partial E \partial \theta} dE d\theta = \frac{g(E)}{2} \sin \theta dE d\theta </math>, | |||
where <math> g(E) </math> is the density of states in three dimensions. | |||
==Problem 3== | |||
'''Quantum point contact conductance:''' When the size of the contact from Problem 3 becomes comparable to the Fermi wavelength <math> \lambda_F = 2\pi/k_F </math>, the contact enters the quantum regime where its conductance becomes quantized as defined by the Landauer formula: | |||
<math> G = \frac{2e^2}{h} \sum_{n=1}^N T_n = N </math>. | |||
Here <math> N </math> is the number of "conducting channels" assumed to have perfect transmission <math> T_n =1 </math> in ballistic transport at zero temperture. One can also view the Sharvin formula from Problem 3 as a limiting case of such Landauer formula where the number of channels | |||
<math> N_{\mathrm{classical}} = \frac{k_F^2 A}{4 \pi} </math> (in three dimensions) is very large, so that <math> N_{\mathrm{classical}}</math> is a continuous function of <math> k_F </math> (rather than discrete <math> N </math> in the Landauer formula above). | |||
Find resistance in Ohm of such contact modeled by a two-dimensional wire (joining the macroscopic reservoirs) in the form of a strip of width <math> W = 1.75 \lambda_F </math>. Assume that conduction electrons in the wire can be described by the free-particle Schrodinger equation with hard-wall [i.e., <math> \Psi(\mathbf{r})=0 </math>] boundary conditions along the lateral edges of the strip. | |||
== Problem 4== | |||
[[Image:qpc_exp.png||thumb|left|400px|Exerimental discovery of conductance quantization in quantum point contacts within 2DEG and temperature effects.]] | |||
'''Finite temperature effects on conductance quantization:''' Suppose that a quantum wire can be modeled by a 2D strip with hard-wall boundary conditions in the direction transverse to the current flow. The width of the wire is <math> a=100 </math> nm and the effective mass of electrons is <math> m^* = 0.067m_0 </math> of the bare electron mass <math> m_0 </math> (which is the case for GaAs heterostructures). | |||
a) Plot the conductance of such a wire as function of the Fermi energy for a number of temperatures <math> T < E_F </math>. The Landauer formula for conductance at finite temperature is: | |||
<math> G(E_F) = \frac{2e^2}{h} \sum_{n=1}^{N_{\rm open}} \int\limits_{-\infty}^{+\infty} dE\, \left(-\frac{\partial f }{\partial E} \right) T_n(E) </math> | |||
where <math> f(E) </math> is the Fermi-Dirac distribution function and <math> T_n(E) = \theta (E-\varepsilon_n) </math> [<math> \theta(x) </math> is the step function] since in ballistic wires a channel is either open (when the Fermi energy is above the bottom of the corresponding subband) or closed (otherwise). | |||
For the plot <math> G(E_F) </math> you can select an interval of Fermi energies encompassing up to 5 subband bottoms <math> \varepsilon_6 > E_F \ge 0 </math> determined by the hard-wall boundary conditions as <math> \varepsilon_n = \frac{\hbar^2 n^2 \pi^2}{ 2m^*a^2} </math>. Express all relevant energies in your plot (<math> E_F </math> along the x-axis, <math> k_B T </math> as parameter, and <math> \varepsilon_n </math> as discrete energies along the x-axis at conductance jumps at zero temperature in steps of <math> 2e^2/h </math>) in units of eV. | |||
b) Using your plot or analytical considerations, determine characteristic temperature(s) at which features of the quantization plateaux begin to disappear. In the latter case, for simplicity, you can consider only the first two subbands (i.e., conducting channels), <math> n=1,2 </math> to obtain explicit analytical expression for <math> G(E_F,T) </math>. How does your conclusion compare to experimental observation, shown in the Figure on the left, of washing out of quantized conductance steps with increasing temperature? | |||
Revision as of 09:24, 24 October 2016
Problem 1
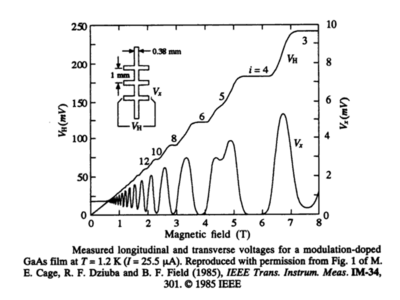
Shubnikov-de Haas oscillations in 2DEG: The physical properties of a 2DEG can be measured by embedding it into a multiterminal Hall bridge, as shown in the Figure above. The energy spectrum of 2D electrons in magnetic field orthogonal to such bridge consists of discrete Landau lavels:
,
which are well-separated for large enough B. Thus, the step-like density of states associated with 2DEG ( is the lowest level in the triangular potential that confines 2DEG) is then broken up into a series of peaks spaced by :
. (1)
Although the spikes are ideally delta functions, scattering processes spread them out in energy. As one changes the magnetic field B, longitudinal voltage (from which one computes the longitudinal resisitivity ) in the Figure above goes through one cycle of oscillations as the Fermi energy moves from the center of one Landau level to the center of the next Landau level. These oscillations are refered to as the Shubnikov-de Haas (SdH) oscillations.
(a) Devise a procedure that will allow you to extract electron density in 2DEG from the values of magnetic field B at which (or the corresponding ) reaches maximum in the course of SdH oscillations.
(b) What is for the 2DEG in the Figure above?
HINT: From Eq. (1) we see that the number of occupied Landau levels is , if electron density is already known.
Problem 2

Classical point contact conductance: The Sharvin formula for the electrical conductance of an extremely short contact area between two pieces of metal is given by
where is the Fermi wavelength. Derive the Sharvin formula by considering the total current flowing through a hole of area in a thin insulating barrier separating two free electron gases with different Fermi energies, as shown in the Figure above. The gas on the left has Fermi energy , while the gas on the right has Fermi energy , where is the applied voltage bias.
Use purely macroscopic arguments:
1) The total current through the contact is
where current density along the z-axis is (carried by electrons within the bias window to ):
.
2) In a free electron gas, the number of electrons with energies between and traveling at an angle between and with respect to a given axis is
,
where is the density of states in three dimensions.
Problem 3
Quantum point contact conductance: When the size of the contact from Problem 3 becomes comparable to the Fermi wavelength , the contact enters the quantum regime where its conductance becomes quantized as defined by the Landauer formula:
.
Here is the number of "conducting channels" assumed to have perfect transmission in ballistic transport at zero temperture. One can also view the Sharvin formula from Problem 3 as a limiting case of such Landauer formula where the number of channels (in three dimensions) is very large, so that is a continuous function of (rather than discrete in the Landauer formula above).
Find resistance in Ohm of such contact modeled by a two-dimensional wire (joining the macroscopic reservoirs) in the form of a strip of width . Assume that conduction electrons in the wire can be described by the free-particle Schrodinger equation with hard-wall [i.e., ] boundary conditions along the lateral edges of the strip.
Problem 4

Finite temperature effects on conductance quantization: Suppose that a quantum wire can be modeled by a 2D strip with hard-wall boundary conditions in the direction transverse to the current flow. The width of the wire is nm and the effective mass of electrons is of the bare electron mass (which is the case for GaAs heterostructures).
a) Plot the conductance of such a wire as function of the Fermi energy for a number of temperatures . The Landauer formula for conductance at finite temperature is:
where is the Fermi-Dirac distribution function and [ is the step function] since in ballistic wires a channel is either open (when the Fermi energy is above the bottom of the corresponding subband) or closed (otherwise).
For the plot you can select an interval of Fermi energies encompassing up to 5 subband bottoms determined by the hard-wall boundary conditions as . Express all relevant energies in your plot ( along the x-axis, as parameter, and as discrete energies along the x-axis at conductance jumps at zero temperature in steps of ) in units of eV.
b) Using your plot or analytical considerations, determine characteristic temperature(s) at which features of the quantization plateaux begin to disappear. In the latter case, for simplicity, you can consider only the first two subbands (i.e., conducting channels), to obtain explicit analytical expression for . How does your conclusion compare to experimental observation, shown in the Figure on the left, of washing out of quantized conductance steps with increasing temperature?