Temp HW 4

Pick problem 1 and three other problems among 2,3,4,5, and 6. Students who try to solve all six problems will be given extra credit.

Problem 1

The two-dimensional electron gas (2DEG) in semiconductor heterostructures with structural inversion asymmetry in the growth direction (perpendicular to the 2DEG plane) plays an essential role in the pursuit of "spintronics without magnetism" since the spin of an electron in nanostructures made of such 2DEGs can be controlled by electrical fields (which can be controlled on much smaller spatial and temporal scales than traditional cumbersome magnetic fields). Such control is made possible by the spin-orbit (SO) couplings which represent manifestations of relativistic quantum mechanics in solids (enhanced, when compared to corrections in vacuum, by the band structure effects).

The important SO coupling for 2DEGs are the linear Rashba and Dresselhaus ones, encoded by the following effective mass Hamiltonian:

${\hat {H}}={\frac {{\hat {p}}_{x}^{2}+{\hat {p}}_{y}^{2}}{2m^{*}}}+{\frac {\alpha }{\hbar }}\left({\hat {p}}_{y}{\hat {\sigma }}_{x}-{\hat {p}}_{x}{\hat {\sigma }}_{y}\right)+{\frac {\beta }{\hbar }}\left({\hat {p}}_{x}{\hat {\sigma }}_{x}-{\hat {p}}_{y}{\hat {\sigma }}_{y}\right)$, (1)

where $\alpha$ measures the strength of the Rashba coupling and $\beta$ measures the strength of the Dresselhaus coupling. Here $({\hat {p}}_{x},{\hat {p}}_{y})$ is the two-dimensional momentum operator and ${\hat {\mathbf {\sigma } }}=({\hat {\sigma }}_{x},{\hat {\sigma }}_{y},{\hat {\sigma }}_{z})$ is the vector of Pauli spin matrices. In GaAs quantum wells the two terms are of the same order of magnitude, while the Rashba SO coupling dominates in narrow band-gap InAs-based structures [the relative strength $\alpha /\beta$ can be extracted from, e.g., photocurrent measurements, Phys. Rev. Lett. 92, 256601 (2004)].

a) Assume a toy model of 1DEG with the Rashba coupling described by the Hamiltonian:

${\hat {H}}_{\rm {R}}^{\rm {1D}}={\frac {{\hat {p}}_{x}^{2}}{2m^{*}}}-{\frac {\alpha }{\hbar }}{\hat {p_{x}}}{\hat {\sigma }}_{y}.$ (2)

Find its eigenstates and eigenvalues as a function of $k_{x}$ (note that $k_{x}=p_{x}/\hbar$ labels the eigenstates since Hamiltonian commutes with the operator ${\hat {p}}_{x}$, $[{\hat {H}}_{\rm {R}}^{\rm {1D}},{\hat {p}}_{x}]=0$ ). Using Mathematica or Matlab, plot both "branches" of $E(k_{x})$.

b) For the Rashba-dominated 2DEG, $\alpha >0$, $\beta =0$, find eigenstates and eigenvalues of the Hamiltonian (1) and use Mathematica or Matlab to plot the corresponding $E(k_{x},k_{y})$ dispersion surface.

c) What is the expectation value $\langle \Psi _{\pm }(\mathbf {k} )|\hbar {\hat {\mathbf {\sigma } }}/2|\Psi _{\pm }(\mathbf {k} )\rangle$ of the spin operator $\hbar {\hat {\mathbf {\sigma } }}/2$ in the eigenstates of spin-split 1DEG in a) and spin-split 2DEG in b)?

d) For $\alpha =\beta$ in the Hamiltonian (1), a spin-helix state of 2DEG can be generated [recently confirmed experimentally, Nature 458, 610 (2009)] within which spins become immune to relaxation. Transform such Hamiltonian into the diagonal form given by Eq. (2) in Phys. Rev. Lett. 97, 236601 (2006), and write explicitly its eigenvalues and eigestates.

REFERENCE: B. K. Nikolić, L. P. Zarbo, and S. Souma, Spin currents in semiconductor nanostructures: A nonequilibrium Green-function approach, Chapter 24 in Volume I of "The Oxford Handbook on Nanoscience and Technology: Frontiers and Advances" (Oxford University Press, Oxford, 2010).

Problem 2

Magnetoelectric effect: The spin accumulation in 2DEG described by the Rashba spin-split Hamiltonian (1), with $\alpha \neq 0$ and $\beta =0$, is zero in equilibrium since SO coupling does not break the time-reversal invariance and spin changes it sign under such operation (therefore, since $\mathbf {S} =-\mathbf {S}$ in time-reversal invariant systems, $\mathbf {S} \equiv 0$). The non-zero spin accumulation within the Rashba-coupled 2DEG can be generated by the application of in-plane electric field [as confirmed in the recent experiments, e.g., Journal of Magnetism and Magnetic Materials 300, 127 (2006)].

Find the relation between $\langle \mathbf {S} \rangle$ and the applied electric field $\mathbf {E} =(E_{x},E_{y})$ in the xy-plane of the 2DEG by using equation for spin density in 2D:

$\langle \mathbf {S} \rangle =\int {\frac {d^{2}\mathbf {k} }{(2\pi )^{2}}}f(\mathbf {k} )\langle \Psi _{\mathbf {k} }^{\pm }|\hbar {\hat {\mathbf {\sigma } }}/2|\Psi _{\mathbf {k} }^{\pm }\rangle$,

that is analogous (i.e., density of states X the filling factor for each state X the value of the physical quantity in each state) to the equation for electron density introduced at the beginning of the PHYS824 course.

The nonequilibrium distribution function in the linear response approximation (i.e., to first order in the electric field) is given by:

$f_{\pm }(\mathbf {k} )=f_{0}(\varepsilon _{\mathbf {k} })+\tau f'(\varepsilon _{\mathbf {k} })\mathbf {E} \cdot \nabla \varepsilon _{\pm }(\mathbf {k} )$,

for either of the two $\pm$ spin-split bands found in Problem 1:

${\hat {H}}_{\mathrm {Rashba} }|\Psi _{\mathbf {k} }^{\pm }\rangle =\varepsilon _{\pm }(\mathbf {k} )|\Psi _{\mathbf {k} }^{\pm }\rangle$.

Here $f_{0}(\varepsilon _{\mathbf {k} })$ is the equilibrium Fermi-Dirac distribution function and $\tau$ is the mean-free time.

NOTE: This means that the general expression for the bulk spin density above reduces in this case to a sum of two terms:

$\langle \mathbf {S} \rangle =\int {\frac {d^{2}\mathbf {k} }{(2\pi )^{2}}}f_{+}(\mathbf {k} )\langle \Psi _{\mathbf {k} }^{+}|\hbar {\hat {\mathbf {\sigma } }}/2|\Psi _{\mathbf {k} }^{+}\rangle +\int {\frac {d^{2}\mathbf {k} }{(2\pi )^{2}}}f_{-}(\mathbf {k} )\langle \Psi _{\mathbf {k} }^{-}|\hbar {\hat {\mathbf {\sigma } }}/2|\Psi _{\mathbf {k} }^{-}\rangle$.

You can test correctness of your expression by checking that it goes to zero for vanishing SO coupling $\alpha \rightarrow 0$.

Problem 3

Shubnikov-de Haas oscillations in the longitudinal voltage.

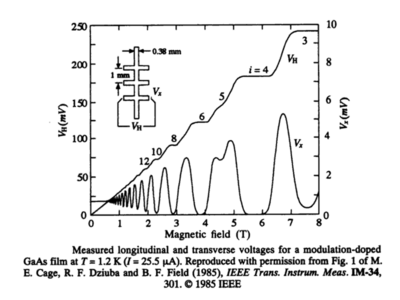
Shubnikov-de Haas oscillations in 2DEG: The physical properties of a 2DEG can be measured by embedding it into a multiterminal Hall bridge, as shown in the Figure above. The energy spectrum of 2D electrons in magnetic field $\mathbf {B} =B{\hat {z}}$ orthogonal to such bridge consists of discrete Landau lavels:

$E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right),\ \omega =eB/m^{*}$,

which are well-separated for large enough B. Thus, the step-like density of states associated with 2DEG $g(E)={\frac {m^{*}}{\pi \hbar ^{2}}}\theta (E-E_{b})$ ($E_{b}$ is the lowest level in the triangular potential that confines 2DEG) is then broken up into a series of peaks spaced by $\hbar \omega$:

$g(E,B)={\frac {2eB}{h}}\sum _{n=0}^{\infty }\delta \left[E-E_{b}-\hbar \omega \left(n+{\frac {1}{2}}\right)\right]$. (1)

Although the spikes are ideally delta functions, scattering processes spread them out in energy. As one changes the magnetic field B, longitudinal voltage (from which one computes the longitudinal resisitivity $\rho _{xx}=V_{x}W/IL$) in the Figure above goes through one cycle of oscillations as the Fermi energy moves from the center of one Landau level to the center of the next Landau level. These oscillations are refered to as the Shubnikov-de Haas (SdH) oscillations.

(a) Devise a procedure that will allow you to extract electron density $n$ in 2DEG from the values of magnetic field B at which $V_{x}$ (or the corresponding $\rho _{xx}$) reaches maximum in the course of SdH oscillations.

(b) What is $n$ for the 2DEG in the Figure above?

HINT: From Eq. (1) we see that the number of occupied Landau levels is $n/(2eB/h)$, if electron density $n$ is already known.

Problem 4

Model of a classical point contact between two massive metallic electrodes.

Classical point contact conductance: The Sharvin formula for the electrical conductance of an extremely short contact area $A$ between two pieces of metal is given by

$G={\frac {2e^{2}}{h}}{\frac {k_{F}^{2}A}{4\pi }}$

where $k_{F}$ is the Fermi wavelength. Derive the Sharvin formula by considering the total current flowing through a hole of area $A$ in a thin insulating barrier separating two free electron gases with different Fermi energies, as shown in the Figure above. The gas on the left has Fermi energy $E_{F}+eV$, while the gas on the right has Fermi energy $\varepsilon _{F}^{0}$, where $V$ is the applied voltage bias.

Use purely macroscopic arguments:

1) The total current through the contact is

$I=j_{z}A$

where current density along the z-axis is (carried by electrons within the bias window $E_{F}$ to $E_{F}+eV$):

$j_{z}=e\int _{E_{F}}^{E_{F}+eV}dE\,\int d\theta v_{z}{\frac {\partial ^{2}n}{\partial E\partial \theta }}$.

2) In a free electron gas, the number of electrons with energies between $E$ and $E+dE$ traveling at an angle between $\theta$ and $\theta +d\theta$ with respect to a given axis is

${\frac {\partial ^{2}n}{\partial E\partial \theta }}dEd\theta ={\frac {g(E)}{2}}\sin \theta dEd\theta$,

where $g(E)$ is the density of states in three dimensions.

Problem 5

Quantum point contact conductance: When the size of the contact from Problem 3 becomes comparable to the Fermi wavelength $\lambda _{F}=2\pi /k_{F}$, the contact enters the quantum regime where its conductance becomes quantized as defined by the Landauer formula:

$G={\frac {2e^{2}}{h}}\sum _{n=1}^{N}T_{n}=N$.

Here $N$ is the number of "conducting channels" assumed to have perfect transmission $T_{n}=1$ in ballistic transport at zero temperture. One can also view the Sharvin formula from Problem 3 as a limiting case of such Landauer formula where the number of channels $N_{\mathrm {classical} }={\frac {k_{F}^{2}A}{4\pi }}$ (in three dimensions) is very large, so that $N_{\mathrm {classical} }$ is a continuous function of $k_{F}$ (rather than discrete $N$ in the Landauer formula above).

Find resistance in Ohm of such contact modeled by a two-dimensional wire (joining the macroscopic reservoirs) in the form of a strip of width $W=1.75\lambda _{F}$. Assume that conduction electrons in the wire can be described by the free-particle Schrodinger equation with hard-wall [i.e., $\Psi (\mathbf {r} )=0$] boundary conditions along the lateral edges of the strip.

Problem 6

Exerimental discovery of conductance quantization in quantum point contacts within 2DEG and temperature effects.

Finite temperature effects on conductance quantization: Suppose that a quantum wire can be modeled by a 2D strip with hard-wall boundary conditions in the direction transverse to the current flow. The width of the wire is $a=100$ nm and the effective mass of electrons is $m^{*}=0.067m_{0}$ of the bare electron mass $m_{0}$ (which is the case for GaAs heterostructures).

a) Plot the conductance of such a wire as function of the Fermi energy for a number of temperatures $T<E_{F}$. The Landauer formula for conductance at finite temperature is:

$G(E_{F})={\frac {2e^{2}}{h}}\sum _{n=1}^{N_{\rm {open}}}\int \limits _{-\infty }^{+\infty }dE\,\left(-{\frac {\partial f}{\partial E}}\right)T_{n}(E)$

where $f(E)$ is the Fermi-Dirac distribution function and $T_{n}(E)=\theta (E-\varepsilon _{n})$ [$\theta (x)$ is the step function] since in ballistic wires a channel is either open (when the Fermi energy is above the bottom of the corresponding subband) or closed (otherwise).

For the plot $G(E_{F})$ you can select an interval of Fermi energies encompassing up to 5 subband bottoms $\varepsilon _{6}>E_{F}\geq 0$ determined by the hard-wall boundary conditions as $\varepsilon _{n}={\frac {\hbar ^{2}n^{2}\pi ^{2}}{2m^{*}a^{2}}}$. Express all relevant energies in your plot ($E_{F}$ along the x-axis, $k_{B}T$ as parameter, and $\varepsilon _{n}$ as discrete energies along the x-axis at conductance jumps at zero temperature in steps of $2e^{2}/h$) in units of eV.

b) Using your plot or analytical considerations, determine characteristic temperature(s) at which features of the quantization plateaux begin to disappear. In the latter case, for simplicity, you can consider only the first two subbands (i.e., conducting channels), $n=1,2$ to obtain explicit analytical expression for $G(E_{F},T)$. How does your conclusion compare to experimental observation, shown in the Figure on the left, of washing out of quantized conductance steps with increasing temperature?