Lattice constant, DOS, and band structure of Si

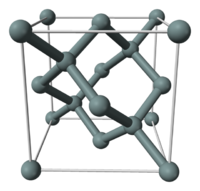
Lattice constant of Si

For bulk materials it is a common task in DFT calculations, given an atomic structure, to find the equilibrium volume of the unit cell. Here we study Silicon which has diamond lattice structure shown in the Figure below:

Diamond cubic crystal structure of silicon.

To determine the equilibrium volume and thereby the lattice constant $a$, a series of calculations is made where $a$ is swept over a range around some initial guess (below we start from $a=5.43$ Angstrom and sweep the lattice parameter $\pm 5\%$ in five steps).

• si_lattice.py

import numpy as np
from ase import Atoms
from ase.lattice import bulk
from ase.io.trajectory import PickleTrajectory
from ase.optimize.bfgs import BFGS
from gpaw import GPAW
from gpaw import PW
from gpaw import FermiDirac

silicon = bulk('Si', 'diamond', a=5.459)

cell = silicon.get_cell()
traj = PickleTrajectory('silicon.traj', 'w')

calc=GPAW(mode=PW(200),                # Energycutoff for planewaves [eV]
          h=0.2,                       # The distance between gridpoints AA^-1
          xc='PBE',                    # xc-functional
          nbands=8,                    # number of bands
          kpts=(2,2,2),                # number of k-points
          occupations=FermiDirac(0.1), # Fermi temperature [eV]
          txt='sibulk_a.txt')
          
silicon.set_calculator(calc)

for x in np.linspace(0.95, 1.05, 7):
silicon.set_cell(cell * x, scale_atoms=True)
traj.write(silicon)

After the calculation has finished, you may analyze the results using the following script:

• plot_eos.py

from ase.io import read
from ase.units import kJ
from ase.utils.eos import EquationOfState

configs = read('silicon.traj@0:7') # read 7 configurations

# Extract volumes and energies:
volumes = [atoms.get_volume() for atoms in configs]
energies = [atoms.get_potential_energy() for atoms in configs]
eos = EquationOfState(volumes , energies)
v0, e0, B = eos.fit()

print v0, 'AA', B / kJ * 1.0e24, 'GPa'
eos.plot('Silicon-eos.png')

The information is stored in silicon.traj file which we will use for post processing. Open the trajectory file with:

ase-gui silicon.traj 

and choose ’Tools’ ! ‘Bulk modulus’. This will produce a fit of the energy vs. unit cell volume for the five calculations, the bulk modulus B and equilibrium volume V0 can be read from the plot title. Be sure to calculate the equilibrium lattice constant a from V0 as we will use it for all subsequent calculations on Silicon.

You can redo the above calculations by increasing the plane wave cutoff in steps of 100 eV until you reach 500 eV, and by increasing the k-point mesh in steps of two until you reach 12x12x12. This should allow you to check how the lattice constant and Bulk modulus converge with respect to the number of plane waves and k-points.

Density of States

To calculate the Density of States (DOS), we start from our previous calculation and increase the number of k-points in a second calculation as the DOS converges slowly with respect to the k-point sampling.

• si_dos.py

import numpy as np
from ase import Atoms
from ase.lattice import bulk
from ase.io.trajectory import PickleTrajectory
from ase.optimize.bfgs import BFGS
from gpaw import GPAW
from gpaw import PW
from gpaw import FermiDirac

silicon = bulk('Si', 'diamond', a=5.459)

calc=GPAW(mode=PW(400),                # Energycutoff for planewaves [eV]
          h=0.2,                       # The distance between gridpoints AA^-1
          xc='PBE',                    # xc-functional
          nbands=20,                   # number of bands
          kpts=(20,20,20),             # number of k-points
          occupations=FermiDirac(0.1), # Fermi temperature [eV]
          txt='sibulk_dos.txt')

silicon.set_calculator(calc)
silicon.get_potential_energy()
calc.write('silicon.gpw', mode='all')

To plot the DOS, you can use ASE utility function:

• plot_dos.py

from ase import *
from ase.dft.dos import DOS
from gpaw import GPAW , restart
import pylab as p

slab , calc = restart('silicon.gpw')
e, dos = calc.get_dos(spin=0, npts=2001, width=0.1)
e_f = calc.get_fermi_level()

p.subplot(211)
p.plot(e-e_f, dos)
p.grid(True)
p.axis([-15, 10, None , None])
p.ylabel('DOS')

p.subplot(212)
p.plot(e-e_f, dos)
p.grid(True)
p.axis([-1, 1, None , None])
p.ylabel('DOS')
p.show()

You can repeat the same calculation using xc='LDA'. Note that neither the LDA nor the GGA are able to calculate the badgap with any high accuracy (there are even examples were semiconductors becomes metallic when using local and semi-local exchange-correlation functionals).

Electronic band structure

To calculate the electronic band structure of Si, we also use the constant charge density mode in DFT and calculate the energy spectra along a number of high-symmetry lines in the Brillouin-zone using the following script:

• si_bands.py

import pickle
import numpy as np
from ase.dft.kpoints import ibz_points , get_bandpath
from gpaw import GPAW

points = ibz_points['fcc']

G = points['Gamma']
X = points['X']
W = points['W']
K = points['K']
L = points['L']

calc = GPAW('silicon.gpw',
             txt='bands_out.txt',
             parallel={'domain': 1},
             fixdensity=True,
             usesymm=None,
             maxiter=150,
             convergence={'bands': 12})
             kpts , x, X = get_bandpath([W, L, G, X, W, K], calc.atoms.cell)

calc.set(kpts=kpts)
calc.get_potential_energy()

e_kn = np.array([calc.get_eigenvalues(k) for k in range(len(kpts))])
pickle.dump((x, X, e_kn), open('eigenvalues.pckl', 'w'))

The result can be post-processed to produce a plot using:

• plot_bands.py

import pickle
import matplotlib.pyplot as plt

point_names = ['W', 'L', '\Gamma', 'X', 'W', 'K']
x, X, e_kn = pickle.load(open('eigenvalues.pckl'))
e_kn -= e_kn[:, :8].max()
emin = e_kn.min() - 1
emax = 1

plt.figure(figsize=(6, 4))
for n in range(8):
plt.plot(x, e_kn[:, n])
for p in X:
plt.plot([p, p], [emin , emax], 'k-')
plt.xticks(X, ['$%s$' % n for n in point_names])
plt.axis(xmin=0, xmax=X[-1], ymin=emin , ymax=emax)
plt.xlabel('k-vector')
plt.ylabel('Energy (eV)')
plt.title('PBE bandstructure of Silicon')
plt.savefig('bs-PBE.png')

About k-point sampling in GPAW

The fact that the periodicity is an inherent feature of a crystal structure, has very important consequences for the numerical treatment of such structures; these must be considered when we calculate periodic systems using any DFT code.

The fact that a crystal is invariant in certain directions with respect to translations by a unit cell length implies that the wave vector is a conserved quantity (note that, you can have 1D and 2D periodic systems also). As a result, the eigenfunctions obey Bloch theorem and are therefore labeled by the wave vector $\mathbf {k}$ (in 1D, k is just a scalar, the wave number k). This also means that the Schrödinger equation can be solved independently for each possible value of $\mathbf {k}$.