Project 2

Deterministic chaos in conservative dynamical system of two balls in one dimension with gravity

Consider a one-dimensional system that consists of two balls moving along the x-axis in response to gravity, as illustrated in the figure below:

A simple dynamical system with two degrees of freedom consists of two point masses or balls constrained to move in one dimension above a floor in a constant gravitational field. Due to assumed elastic collisions, the system exhibits discontinuities as a function of time.

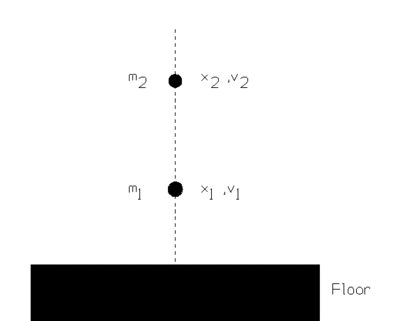
Collisions between the balls and between the lower ball and the floor are completely elastic, i.e., this is a conservative Hamiltonian system.

Write a program to follow the motion of both balls, where you have to pay special attention to the collision events at which the motion changes abruptly. You can do this either

(a) Suggested for PHYS460 students: by using finite difference midpoint method (which actually yields exact, but discretized, solution for motions with constant acceleration):

$v_{1,i+1}=v_{1,i}-g\Delta t$

$x_{1,i+1}=x_{1,i}+{\frac {v_{1,i+1}+v_{1,i}}{2}}\Delta t$

$v_{2,i+1}=v_{2,i}-g\Delta t$

$x_{2,i+1}=x_{2,i}+{\frac {v_{2,i+1}+v_{2,i}}{2}}\Delta t$

or

(b) Suggested for PHYS660 students: exactly, i.e., without using finite difference equations if you can look ahead and calculate exact times and positions of the collisions.

When the collision with the floor occurs, you should reverse the velocity of the lower ball. On the other hand, when the balls collide with each other, you should use the formula for elastic collisions of two objects (derived in elementary classical mechanics) to find their velocities after the collision.

Part I for both PHYS460 and PHYS660 students

For the three cases:

• $m_{2}=0.5m_{1}$
• $m_{2}=m_{1}$
• $m_{2}=9m_{1}$

construct Poincaré sections by plotting $v_{2}$ against $x_{2}$ at times when the two balls collide. Take $m_{1}=1$, and use the initial conditions $x_{1}=1$; $v_{1}=0$; $x_{2}=3$, and $v_{2}=0$. Which, if any, of these plots indicate that the system is chaotic?

Part II for both PHYS460 and PHYS660 students

Find the position and velocities of the two balls at equal time intervals. Plot $x_{2}$ against time $t$ for these three cases.

Part III for both PHYS460 and PHYS660 students

Employ the autocorrelation function

$C(\tau )=\int _{0}^{\infty }[x(t)-{\bar {x}}][x(t+\tau )-{\bar {x}}]dt$

which measures self-similarity of a signal with itself in different time intervals (here ${\bar {x}}$ is the average value of the signal), to analyze the "signal" $x_{2}(t)$ generated by the motion of the second ball. Note that for a discrete set of data composed of N points one should switch to "autocovariance"

$R(\tau )={\frac {1}{N-\tau }}\sum _{n=1}^{N-\tau }x_{n}x_{n+\tau }$

which is essentially a correlation function, except that each point in $R(\tau )$ is normalized by the number of points used to calculate the discrete integral.

Comment on similarities and differences in the three cases above. In general, we expect autocorellation function to be constant or oscillating for regular motions, while it decays fast to zero (typically in exponential fashion) for chaotic motions.

Part IV for PHYS660 students only

Repeart Poincaré section computation in c) for at least 11 additional sets of initial conditions. For example, you can decrease $x_{2}=3$ in steps of $0.1$, while adjusting initial velocities so that the total energy remains the same for each set. Plot all 12 Poincaré sections on the same graph and compare with a single Poincaré section you obtained in I) using just one of these 12 sets of initial conditions.

REFERENCES

• N. D. Whelan, D. A. Goodings, and J. K. Cannizzo, Phys. Rev. A 42, 742 (1990).
• Autocorrelation function of discrete and finite data sets.
• Elementary velocity formulas for elastic collision.